Countable Infinities: The Smallest Infinity There Is

Infinity is certainly a strange thing. Something you may not know, is that there are several different infinities, some which are larger than others. How can something infinitely large still be smaller than something? Let us look at the smallest of the infinities, the countable one, and what makes it differ from other infinities. As examples of infinities, we will hear use sets of numbers, a set simply being any collection of numbers, the size of the sets being the amount of different numbers the set contains.
To Prove it is Countable
To get a grasp of what a countable infinity is, let us start with the definition. The natural numbers, that is to the set of numbers 1,2,3,4..... and up to infinity is countably infinite. The requirement for any other infinite series of numbers to be countable is that there is bijection between that series and the natural numbers.
Now, what is a bijection? Simply put, a bijection means a one-to one correspondence, that each number in the first set corresponds to exactly one number in the second set of numbers, and the other way around. You may also look at it as ordering the numbers of the two sets into pairs, with one part of each pair coming from a different set, so that no numbers are left behind.
This is a pretty natural way to define that two amounts are equally large, and for the sake of these sets, it simply means finding a function between the sets pairing up each number. There is another way to think of countable numbers, though: they can be put in an order such that while there is an infinite number of elements, if you go through the list with an element in mind, it will take less than infinite time to find it.
Putting in Order
Again, look at the natural numbers. There are an infinite amount, but if you want to find an element, for example 3.553.532, and you start at 1, there are a finite amount of numbers you have to search through before you find it(there are 3.553.531 numbers you have to look at first, to be exact).
Compare this to an uncountable infinite set, like the real numbers, the number line but with all numbers, like π or 2/4. While difficult to prove, they can not be put in such an order. Imagine starting at 0, and going through all the numbers to find 1. There are an infinite amount of numbers between 0 and 1, so you will never reach it.
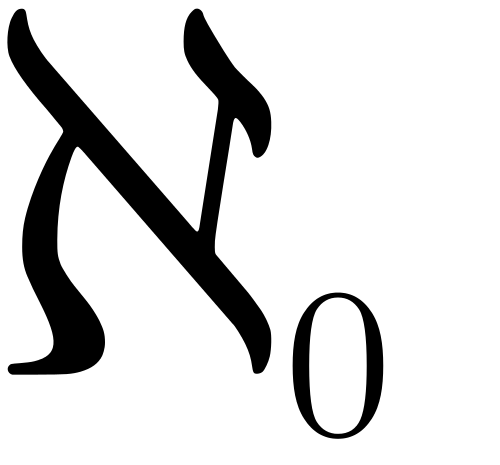
Countable Examples
Back to the countable numbers, let us look at some examples. First, the whole numbers are countable. They consists of the natural numbers, but also 0 and all -1, -2 and so on. It may seem strange that the whole numbers, which contains the natural numbers and more, is exactly as large as the natural numbers, but this is one of the strange things concerning infinity.
The function from one to another is simple. Say x is a whole number. If x is less than 0, take -2×x to be the natural number x is connected to. If x is 0 or larger, pair it up with 2×x+1. As you see, the negative number corresponds to the even numbers in the natural numbers, and the positive is sent to the odd numbers. You may also check that each of the natural numbers is only connected to one whole. If you wish to put the whole numbers in an order such that it conforms to what I wrote earlier, simply do it like this: 0,1,-1,2,-2.... and so forth, and you will arrive at any number in finite steps.
Another weird set which turns out to be countably infinite, is the set N×N. N×N could be seen as coordinates, a two-dimensional map where coordinates are given in natural numbers, like (2,2) or(134, 23). There are as many of these combinations of natural numbers as there are natural numbers, no matter how insane that sounds. The function from N×N to the natural numbers is 2n×(2m-1), (m,n) being a point in N×N. Proving this is a little more complicated, but try if you want.
Uncountable
It may seem difficult to understand what lies beyond the countable infinity. I mentioned the real numbers, but just the real numbers between 0 and 1 are uncountable. In fact, there are as many of them as there are real numbers on the entire number line. And beyond that there are larger infinities, but I shall not try to explain them here. Proving that the real numbers are uncountable is sadly also quite difficult, as you would have to prove that no function between the reals and the naturals could possibly exist, much more difficult than finding a function and then proving that it holds the necessary requirements. Nonetheless, this should have given some understanding of the strange world of infinities we deal with in mathematics.