Creating a linear and quadratic sequence using the nth term formula.
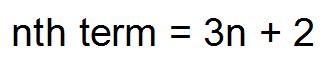
Creating a sequence if given the nth term formula can be done by subbing in the numbers n=1, n=2, n=3, n=4, n=5... into the nth term formula.
Example 1
The nth term of a sequence is 3n + 2. Write down the first 5 numbers.
First make sure you understand the meaning of 3n + 2. It means to get the numbers in the sequence you need to multiply the position number by 3 and add on 2.
First of all sub in n = 1
3 × 1 + 2 = 5
Next sub n = 2
3 × 2 + 2 = 8
Next sub in n = 3
3 × 3 + 2 = 11
Next sub in n = 4
3 × 4 + 2 = 14
Finally, sub in n = 5
3 × 5 + 2 = 17
so the first 5 terms in the sequence are 5,8,11,14,17...
Example 2
The nth term of a sequence is 2n - 9. Write down the first 3 numbers.
First make sure you understand the meaning of 2n - 9. It means to get the numbers in the sequence you need to multiply the position number by 2 and take off 9.
First of all sub in n = 1
2 × 1 - 9 = -7
Next sub n = 2
2 × 2 - 9 = -5
Finally, sub in n = 3
2 × 3 - 9 = -3
so the first 3 terms in the sequence are -7,-5,-3...
Example 3
Find the first 5 terms of the sequence 3n² + 1
Quadratic sequence can be created in a similar way.
First of all sub in n = 1
3 × 1² + 1 = 5
Next sub n = 2
3 × 2² + 1 = 13
Next sub in n = 3
3 × 3² + 1 = 28
Next sub in n = 4
3 × 4² + 1 = 49
Finally, sub in n = 5
3 × 5² + 1 = 76
so the first 5 terms in the sequence are 5,13,28,49,76...
More help from me on sequences:
How to find the nth term of an increasing linear sequence.
Quadratic Sequences. The nth term of a quadratic number sequence.