Differentiating the exponential function. The derivative of e^x.

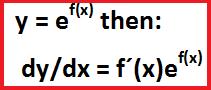
The exponential function is probably one of the easiest functions to differentiate as the derivative is the same function. This means that the derivative of exponential is exponential:

So if y = e^x then dy/dx = e^x

However, a more useful result is this one:

If y = e^f(x) then dy/dx = f´(x)e^f(x)

Example 1

If y = e^7x-4 then work out the derivative of y.

So in this question f(x) = 7x -4 so f´(x) = 7. Also you now that the derivative of exponential is exponential.

So using dy/dx = f´(x)e^f(x) you will get:

dy/dx = 7e^7x-4

Example 2

If y = e^5x+2 then work out the derivative of y.

So in this question f(x) = 5x + 2 so f´(x) = 5. Also you now that the derivative of exponential is exponential.

So using dy/dx = f´(x)e^f(x) you will get:

dy/dx = 5e^5x+2

Example 3

If y = 11e^4x then work out the derivative of y.

So in this question f(x) = 4x so f´(x) = 4. Also you now that the derivative of exponential is exponential.

So using dy/dx = f´(x)e^f(x) you will get:

dy/dx = 11 × 4e^4x = 44e^4x

Example 4

If y = e^cos5x then work out the derivative of y.

So in this question f(x) = cos5x so f´(x) = -5sin5x. Also you now that the derivative of exponential is exponential.

So using dy/dx = f´(x)e^f(x) you will get:

dy/dx = -5sin(5x)e^cos5x

Example 5

If y = e^sinx then work out the derivative of y.

So in this question f(x) = sinx so f´(x) = cosx. Also you now that the derivative of exponential is exponential.

So using dy/dx = f´(x)e^f(x) you will get:

dy/dx = e^sinx cosx

Example 6

If y = -2e^-9x then work out the derivative of y.

So in this question f(x) = -9x so f´(x) = -9. Also you now that the derivative of exponential is exponential.

So using dy/dx = f´(x)e^f(x) you will get:

dy/dx = -2 × -9 × e^-9x = 18e^-9x