The Lorentz Contraction, or, How Motion Affects Space (Part 1)

We are now well informed and knowledgeable about special relativity’s time dilation phenomenon. Furthermore, we have realized that the relativistic distance contraction phenomenon is a direct result of, and always ‘accompanies’, or complements, the time dilation phenomenon – these two physical effects are forever interwoven. Those gritty, high speed muons provided us with an excellent example of this reality. If we recall, from our point of view, it was time dilation that caused the muons to age much more slowly than they normally would, thus enabling them to traverse the entire expanse of our atmosphere and slam into the earth well after their disintegration should have occurred. But from the muons’ point of view, it was the length contraction of the atmosphere that enabled the earth to slam into them well before their impending decay, because, from the muons’ perspective, time, for them, was passing by at the normal rate.
Thought Experiment #2 – How Does Motion Affect Space?
We have already shown that the principle of relativity, that is, the first postulate, and the constancy of the speed of light, that is, the second postulate, combine to cause time dilation, but we have not done the same for the phenomenon of relativistic length contraction, at least, we have not done so with the same “thoroughness”. So we ask ourselves, “Can length contraction be deduced using only special relativity’s two fundamental postulates, just as time dilation was? Specifically, from the standpoint of the postulates, why does length contraction happen in the first place?”.
First, we repeat our earlier thought experiment, but this time, we ask Scotty to bring with him a second photon clock which is completely identical to his original one. He synchronizes both photon clocks so that they are ticking with the same cadence, and promptly boards his train (again), taking them with him. He then positions both clocks so that they are standing vertically and side by side on the passenger car’s floor, such that their photons are traveling up and down between their respective mirrors as they tick, just like before. Scotty now leaves his first photon clock standing in the vertical position. We will call this “Clock V”, since its photon, from Scotty’s point of view, is traveling in the vertical direction, which is a direction that is perpendicular to the direction of motion of his train. He then re-positions his second clock so that, although still directly beside Clock V, it is now lying horizontally on the passenger car’s floor, such that its photon is now traveling forward and backward between the mirrors as it ticks. We will call this “Clock H”, since its photon is traveling in a horizontal direction that is along, or in line with, the direction of motion of Scotty’s train. And so, as Mr. Scott observes both of his clocks blissfully ticking away, the T.O. Special shoots through the train crossing once more, traveling with uniform motion from left to right at the relative speed v, which is close to the speed of light c. Now, from our vantage point standing at the train crossing, we again see Clock V’s photon take its usual double diagonal path as it completes each tick, as shown in Figure 1.1 by the dashed blue lines.
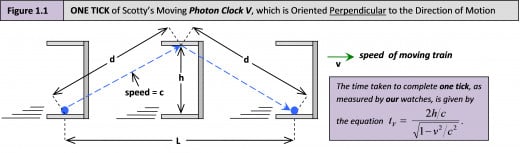
And just as before, we observe that Clock V is ticking at a slower rate than our stationary photon clock by a factor of

that is, the relativistic time dilation factor.
Also, we recall that we had previously derived, from our first thought experiment about time dilation, that the amount of time it takes, as observed from our point of view, that is, as measured by us using our watches, for Clock V’s photon to complete 1 tick, is given by the equation

Here, “V” denotes Clock V, h is the distance between the reflective surfaces of the mirrors, v is the relative speed of Scotty’s train, and c is, of course, the speed of light (to refresh our memory, we can quickly review our derivation of the time dilation factor, in which we labeled the above equation for tV as “Eqn (2)”). Nothing new here, just reminiscing ‘old times’. However, for reasons that will become self-evident, we will change the form of our equation slightly, by dividing both the numerator and the denominator by the speed of light, c. Doing so obviously does not change our equation’s value whatsoever, but yields the new form:

We will soon be using this equation and the equation for Clock H, which we will now derive, to surprising effect, so let’s keep the former well wedged in our brains as well.[1]
Thought Experiment #2 – Clock H’s Photon’s Left To Right Journey
“That’s nice, but what about Clock H?”, we ask. Well, our next logical step is to derive the equation for the total amount of time that it takes, again, as observed from our point of view, that is, as measured by us using our watches, for Scotty’s horizontal Clock H to complete 1 tick, just as we did for his Clock V in our thought experiment on time dilation, with one of the results being our equation for tV. Since Scotty’s train is moving through the crossing from left to right, our strategy will be to first calculate the travel time of Clock H’s photon as it journeys from the left hand mirror to (strike) the right hand mirror, and then calculate its travel time as it thereafter journeys from the right hand mirror back to (strike) the left hand mirror, thereby registering 1 tick. Once we have calculated these two times, we can simply add them together to obtain the total time that it takes Clock H to complete 1 tick, as observed from our point of view standing at the train crossing.
And so, as the train speeds through the crossing and we carefully note the path of Clock H’s photon, what do we predict that we should observe? Let’s have a look at Figure 1.2 to help us out.
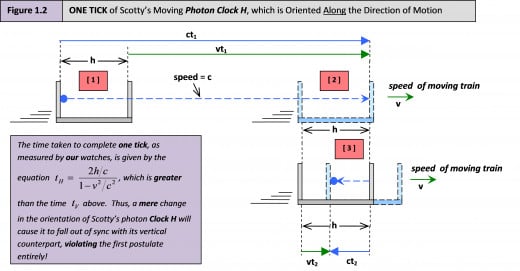
We should observe that the photon first travels from the left hand mirror to the right hand mirror. But since Scotty’s train is already moving to the right at the very high relative speed v which is close to the speed of light c, and since the photon must always travel at the speed of light c, then it will take the photon some time to catch up to and strike the right hand mirror, because in essence, the mirror is “trying to pull away” from the photon at the very high relative speed v. Hence, the photon must travel a comparatively long distance to catch up to the mirror, as shown by the long, dashed blue line. “Okay, so how much time?”, we inquire. Well, let’s look at Figure 1.2 in more detail and work it out…
We let t1 equal the amount of time, as measured by us using our watches, that it takes Clock H’s photon to travel from the left hand mirror to (strike) the right hand mirror. Now, recalling that DISTANCE TRAVELED = SPEED x TRAVEL TIME, then the total distance traveled by the photon when it finally strikes the right hand mirror is thus equal to ct1, as shown by the long, solid blue line in Figure 1.2. But in this same amount of time t1, the right hand mirror (and indeed, the entire photon clock itself) has also traveled to the right, but by a lesser distance equal to vt1, as shown by the long, solid green line, where v is, of course, the speed of Scotty’s train relative to us. Therefore, by studying the simple geometry of Figure 1.2, we can deduce that:

Thought Experiment #2 – Clock H’s Photon’s Right To Left Journey
The photon then bounces off of Clock H’s right hand mirror and now moves leftward at the speed c, where it will soon hit the oncoming left hand mirror and consequently complete its tick, as shown in Figure 1.2. We say “soon”, because Clock H is already moving to the right at the very high relative speed v. Therefore, unlike the right hand mirror that was “trying to pull away” from the photon, the left hand mirror is, in essence, “trying to ram into” the photon at the very high relative speed v. And hence, the amount of time that it takes the photon to make its return journey from the right hand mirror to the left hand mirror will be considerably less than the amount of time t1, traveling a comparatively shorter distance to do so, as shown by the short, dashed blue line. “Okay, fool, so how much time, for the second time?”, we inquire again. Cool it, you jive turkeys, because once more, Figure 1.2 will provide the answer…
Likewise, we let t2 equal the amount of time, as measured by us using our watches, that it takes Clock H’s photon to travel from the right hand mirror to the left hand mirror. And again, recalling that DISTANCE TRAVELED = SPEED x TRAVEL TIME, then the total distance traveled by the photon when it strikes the left hand mirror (and registers a tick) is equal to ct2, as shown by the short, solid blue line in Figure 1.2. But in this same amount of time t2, the left hand mirror has traveled rightward by a distance equal to vt2, as shown by the short, solid green line. Therefore, by again examining the geometry of the situation, as shown by Figure 1.2, we can deduce that:
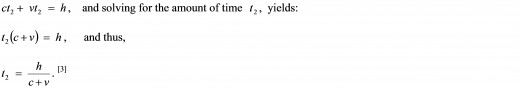
Thought Experiment #2 – Clock H’s Photon’s Complete Left To Right To Left Journey
Consequently, having derived equations for the amounts of time t1 (for the photon’s left hand mirror to right hand mirror journey) and t2 (for the photon’s right hand mirror back to left hand mirror journey), we can now come up with an equation for the total amount of time that it takes, as observed from our point of view, that is, as measured by us using our watches, for Clock H’s photon to complete 1 tick. We will call this total amount of time tH, where “H” denotes Scotty’s horizontal Clock H. Hence, the total amount time, tH, that it takes Clock H to complete 1 tick, as measured from our point of view, is clearly just the sum of the amounts of time t1 and t2. Expressing this mathematically gives us:


Thought Experiment #2 – A Fundamental (and Hopefully Understandable) Mathematical Comparison
Okay. Let us now mathematically compare these two amounts of time tV and tH that it takes Scotty’s Clock V and Clock H to complete their respective ticks, with both amounts having been measured from our point of view. In doing so, we can understand how tV and tH are related, and use this relationship to predict the behaviour of Scotty’s photon clocks, as observed from our point of view. As we have previously derived, these amounts of time are given by the following equations:
1) The amount of time that it takes, as measured by our watches, for Clock V to complete 1 tick is given by:

2) The amount of time that it takes, as measured by our watches, for Clock H to complete 1 tick is given by:

The equations look similar, but they are clearly not the same. And just to remind ourselves, h is the distance between the reflective surfaces of the mirrors, v is the relative speed of Scotty’s train, and c is the universally constant speed of light.
Taking a closer look at these two equations, we notice that the numerators of the times tV and tH are the same, that is, they are both equal to the quantity

Now, recalling that

it is important for us to remember at this point that this quantity, 2h / c, is therefore equal to the amount of time that it takes, as observed from Scotty’s point of view, that is, as measured by him using his watches, for both of his Clocks V and H to complete 1 tick. And why is this so? Well, because of special relativity’s first postulate, Scotty has every justification to claim that he and his train are the ones at rest, while we and the rest of the outside world are the ones moving instead. Therefore, as observed from Scotty’s point of view on board his train, Clock V’s photon travels only up and down in the vertical direction, thus traversing a total distance of only 2h to complete 1 tick. And because of special relativity’s second postulate, Scotty will measure Clock V’s photon to traverse this total distance at the universally constant speed of light c. Hence, he will conclude that the amount of time that it takes Clock V to complete 1 tick is equal to 2h / c. Likewise, as observed from Scotty’s point of view, Clock H’s photon travels equal distances to the right and then to the left in the horizontal direction, thus also traversing a total distance of only 2h at the constant speed of light c, to complete 1 tick. Hence, he will again conclude that the amount of time that it takes Clock H to complete 1 tick is also equal to 2h / c, just as that for Clock V.
Therefore, and this is very important: From Scotty’s point of view on board his train, Clock V and Clock H must and will always remain in synchronization with each other. Although this fact may sound inconsequential at this juncture, as we’ll discover later on, it leads our current comparison of the times tV and tH, which are amounts of time that we have calculated from our point of view, to a complete and utter destruction of the first postulate, whose resolution is the relativistic length contraction phenomenon, that is, the Lorentz Contraction.

Alright. Onward with our comparison… We now notice that the denominators of the times tV and tH are, although similar, not the same. tV's denominator is the quantity sqrt(1 - v2 / c2), while tH's is the quantity 1 - v2 / c2. Similar, but not the same. Now we have already studied the “behavior” of the expression sqrt(1 - v2 / c2) as the relative speed v increases, in our discussion about time dilation. But for the purpose of unraveling the ins and outs of length contraction, it is nevertheless well worth investigating this expression, along with the expression 1 - v2 / c2, in a little more detail this time around. Just before we do so, we note that we are, of course, excluding the “trivial” case where the relative speed v equals zero from our comparison. And this is due to the fact that if v = 0, then the object, that is, Scotty’s train, is at rest with respect to the observer, the observers being us, and hence there can be neither length contraction nor time dilation at work, as observed from our point of view. Continuing on, we see that both denominators contain the quantity 1 - v2 / c2, and since the relative speed v of any material object must always be less than the speed of light c (the reason for which will be discussed in full later on), then the value of v / c must always be less than 1. And if v / c is always less than 1, then it follows that the value of v2 / c2 must also always be less than 1. Not to be repetitive, but if v2 / c2 is always less than 1, then the final result in this logical chain is the fact that the quantity 1 - v2 / c2 must also always be less than 1. Putting it in plain English, “the result of subtracting a quantity whose value is always less than one from a value of one, must always be less than one itself” – makes sense, but it’s an ‘utter’ tongue twister.
So far, so good, we trust. Proceeding further, if a quantity is less than 1, then its square root must be greater than the original quantity itself, but must still be less than 1. For example, the quantity 0.81, which is less than 1, has a square root that is equal to 0.90, since 0.90 x 0.90 = 0.81. Thus, as we can see, the square root of 0.81 is greater than 0.81 itself, but is still less than 1.[4]
And therefore, having spewed that entire mouthful, we can conclude that: Since the quantity 1 - v2 / c2 is always less than 1, as we have just demonstrated, then its square root, which is the quantity sqrt(1 - v2 / c2), must always be greater than 1 - v2 / c2 itself, but must also still be less than 1, as we have also just demonstrated. Hence, for an object, such as Scotty’s train, that is moving at a given relative speed v, the first relationship that

must always be true. Additionally, we mention, for the sake of completeness, that the second relationship that

must also always be true.
Now, knowing this first relationship and taking a look back at our equations for the amounts of time tV and tH, we are led to finally conclude that: The amount of time tH must ALWAYS be greater than the amount of time tV. And why is this so? Because while their respective numerators, both of which equal 2h / c, are the same, tH's denominator, which equals 1 - v2 / c2, must always be less than tV's denominator, which equals sqrt(1 - v2 / c2), as we have just proven. Then from a purely mathematical standpoint, a lesser denominator means a greater quotient, hence our final conclusion that tH > tV.

And so at long last, we can make the following prediction: Because the amount of time that it takes Clock H to complete 1 tick, which is tH, is always greater than the amount of time that it takes Clock V to complete 1 tick, which is tV – with both amounts of time being measured from our point of view, that is, measured by us using our watches – then from our vantage point standing at the train crossing, we will observe that Scotty’s Clock H is ticking at a slower rate than his Clock V! And therefore, as a direct result of Clock H ticking more slowly than Clock V, we will observe that Clock H falls out of its original synchronization with Clock V!
Notes:
[1] We bring to mind that we derived the equation

as part of our more general derivation of the relativistic time dilation factor, in our discussion about time dilation. As we know, the above equation for tV is the equation for the amount of time, as observed from our point of view, that is, as measured by us using our watches, that it takes Scotty’s Clock V to complete 1 tick. It is now worth mentioning that this equation can also be derived by directly using our newfound knowledge of the relativistic time dilation phenomenon. To do so, we once again put ourselves into Scotty’s fragrantly smelling shoes. Now, remembering that

then from Scotty’s point of view, that is, as measured by him using his watches, the amount of time that it takes his Clock V to complete 1 tick is therefore equal to 2h / c instead. And why is this the case? Well, because Scotty has every right to claim that it is he and his train that are the ones at rest, while we and the rest of the outside world are the ones moving past him at the relative speed v. Therefore, as observed from Scotty’s point of view, Clock V’s photon travels only up and down in the vertical direction, thus traversing a total distance of only 2h at the universally constant speed of light c, to complete 1 tick.
Okay, let’s switch back to our point of view. To us, we are the ones at rest, while Scotty and his train are the ones moving past us at the relative speed v. Hence, due to the time dilation phenomenon, we will observe that Scotty’s moving clocks are all ticking at a slower rate than our stationary clocks (which are, to us, of course ticking at the normal rate of time passage), by a factor of

which is the relativistic time dilation factor. Thus, from our point of view, if we observe that Scotty’s moving photon Clock V ticks Δt times, we will observe that our stationary photon clock ticks a corresponding

times, which must necessarily be greater than Δt, because his clocks are ticking more slowly than ours are (and also, because we already know that from a strictly algebraic standpoint, the value of the quantity sqrt(1 - v2 / c2) is always less than 1). And therefore, if we similarly observe an amount of time of 2h / c elapse on Scotty’s (more slowly ticking) moving clocks – which is the amount of time, as measured from his point of view, that it takes Clock V to complete 1 tick – then we must observe a corresponding greater amount of time of

elapse on our (normally ticking) stationary clocks. And so, we clearly see that this last expression is exactly equal to our original expression for the amount of time tV, which is the amount of time – as observed from our point of view, that is, as measured by us using our watches – that it takes Scotty’s Clock V to complete 1 tick!
[2] Since the right hand mirror is moving to the right at the speed v relative to us, and the photon is also moving to the right at the speed of light c relative to us (and to everything else!), then the rate, or speed at which the distance between them is decreasing must equal c – v, as measured from our point of view. And since the initial distance between the mirror and the photon is equal to h, then the amount of time that it takes the photon to catch up with and strike the right hand mirror, as measured from our point of view, must be equal to h / (c - v), since TIME = DISTANCE / SPEED. This is an equivalent way of obtaining the equation for t1.
[3] Since the left hand mirror is moving to the right at the speed v relative to us, but the photon is moving to the left at the speed of light c relative to us (and to everything else!), then the rate, or speed at which the distance between them is decreasing must equal c + v, as measured from our point of view. And since the initial distance between the mirror and the photon is equal to h, then the amount of time that it takes the photon to meet and strike the left hand mirror, as measured from our point of view, must be equal to h / (c + v), since TIME = DISTANCE / SPEED. This is an equivalent way of obtaining the equation for t2.
[4] Actually, any real number greater than zero always has, in fact, two square roots – a positive square root and a negative square root. Thus, from our example, the number 0.81 has two square roots, specifically, +0.90 and -0.90, because 0.90 x 0.90 = 0.81, and (-0.90) x (-0.90) = 0.81 as well. However, for the level of our discussions, we will simply ignore, or discard the negative square root, since it has no “physical” connotation.
Continue To Part 2
- The Lorentz Contraction, or, How Motion Affects Space (Part 2)
The 2nd in a series of articles on Albert Einstein's Special Theory of Relativity
Go Back To "Does Motion Affect The Speed At Which Time Passes? (Part 1)"
- Does Motion Affect The Speed At Which Time Passes? (Part 1)
The 1st in a series of articles on Albert Einstein’s Special Theory of Relativity