Domain and Range of a Function
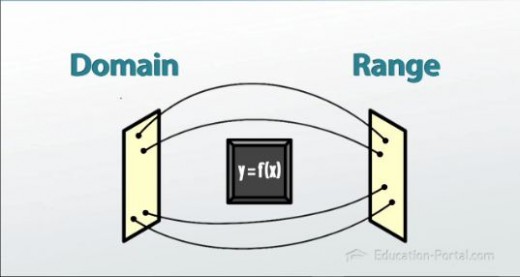
Definition
Domain:
Domain is defined as the set of all those values for which the function is defined.
In other words domain is a set of all those values which when plugged into the function give the result which lies in the real range i.e its neither a complex number nor any undefined form.
By undefined form we mean the forms such as 0/0 , n/0 , infinity/n , infinity/infinity , where n is any number other than 0.
Range:
Range is defined as the set of all those values which result by using the functional formula.
In other words range is a set of all those values which are obtained when the values from domain are plugged into the function.

Suppose we have a function f(x). Then the domain of the the function will be all those possible values of x which can be plugged into the function giving a real ans. Range will be all those values of f(x) which are obtained when different values of x are plugged into the function.
Finding Domain and Range of different Functions
In order to deal with domain and range we can divide the functions into following types:
- Linear Functions
- Quadratic functions
- Functions with degree greater than 2
- Constant Functions
- Functions of the form P(x)/Q(x)
- Functions involving Square root, cube root, fourth root etc
- Trigonometric functions
- Exponential and Logarithmic Functions
1.Linear Functions:
The functions with degree 1 are defined as linear functions.
2x, 2x+6, 8-7x etc all are linear functions because the highest power of the variables involved is 1.
Domain and Range of Linear Functions:
Domain of a linear function is almost always going to be set of all real numbers because there won't be any such value which will give us a complex or undefined form. Similarly the range will also be the set of all real numbers because when we will put the values from entire real domain in result we will get result the values which will be ranging from -infinity to +infinity.
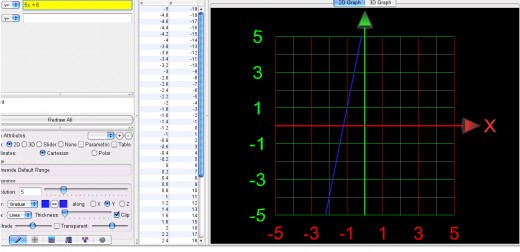
The graph shown below is of a function y= 5x+6. The blue line shows the graph of the function. The x values are the Domain and the y values are the Range. The line will extend forever in either y direction without any break showing the range is from -infinity to +infinity.
2.Quadratic Functions
The functions having a degree two are termed as quadratic functions.
2x2 + 4 , (x+4)2 etc are quadratic functions.
Domain and Range of Quadratic Functions:
Since in this case we can use any value of x i.e we won't get any undefined form or complex ans for any value of x, therefore, the domain in case of quadratic functions is the set of all real numbers i.e. from -infinity to +infinity.
However the case is different in case of Range. Consider a simple function y=x2 .
In this case which ever value of x you put in the equation the value of y will never be negative.
It will always be 0 or greater than 0.
Lets substitute different values of x in this equation:
y=x^2
x
| y
|
|---|---|
-5
| 25
|
-15
| 225
|
-2
| 4
|
0
| 0
|
2
| 4
|
3
| 9
|
y = x^2 + 5
x
| y
|
|---|---|
-5
| 30
|
-10
| 105
|
0
| 5
|
1
| 6
|
4
| 21
|
From the table its clear that value of a quadratic function will never be less than zero, therefore, the range of y=x2 will be from 0 to +infinity.
Now consider any number being added or subtracted from x2. For example y=x2 + 5.
The domain does not change in this case but the range will change. In case of x2 the range was from 0 to +infinity but in this case 5 is being added in every value so the range will be from 5 to +infinity.
Previously y was zero when x was zero. In this case if x is zero then y will be (0)2 + 5 = 5.
The table on the right shows the values of y for different values of x.
The same holds when some number is being subtracted from x2. For example, we have a function y= x2 - 5 . The Domain will be set of all real numbers while the range will be from -5 to +infinity. -5 is obtained when 0 is substituted in the function.
A slightly different case arises when we have a complete square e.g (x+2)2 . In this case first the number is being added in x and then we are taking the square. It becomes similar to simple x2 .
The Domain in this case will again be set of all real numbers while the range will be from 0 to +infinity.
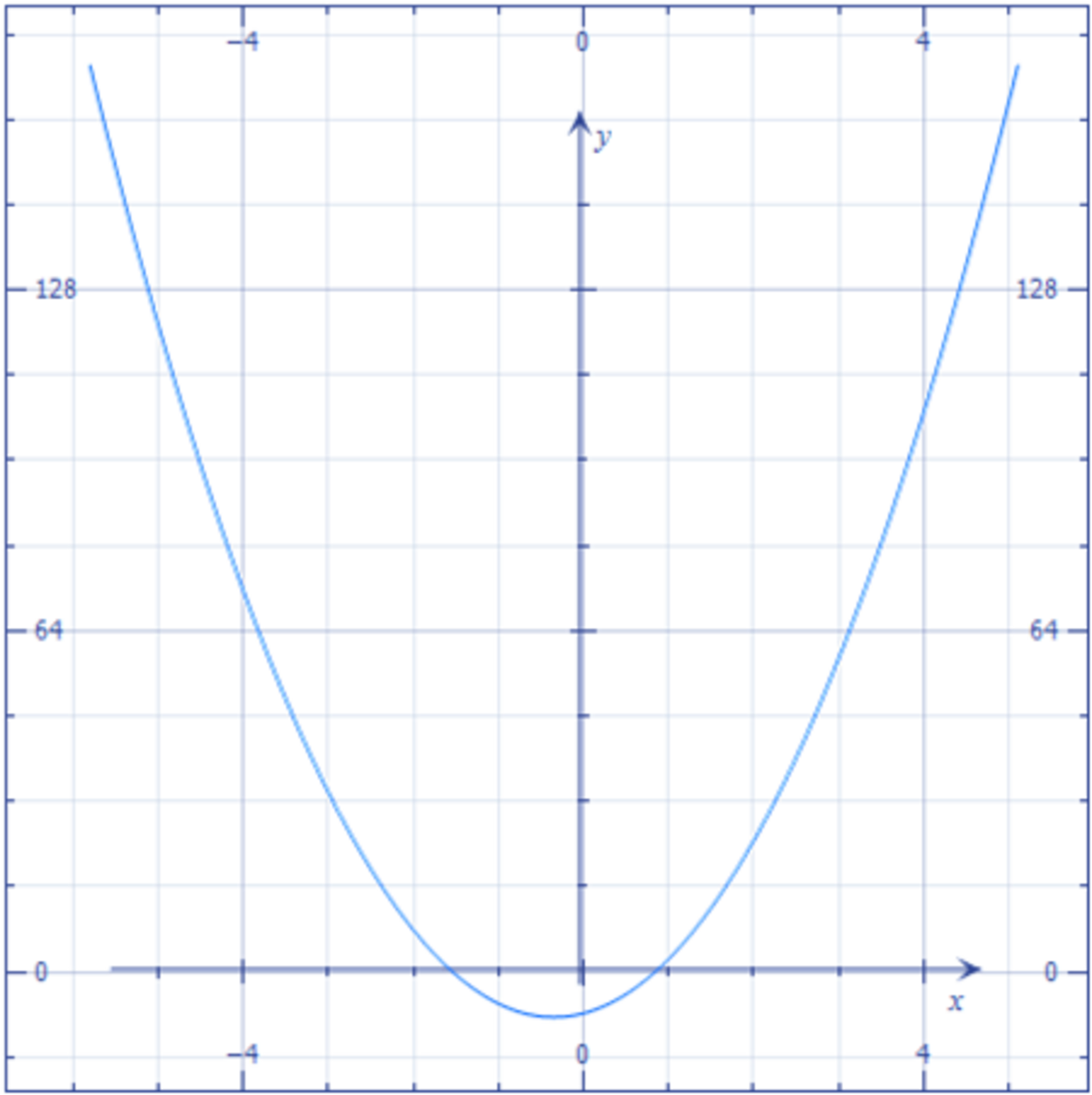
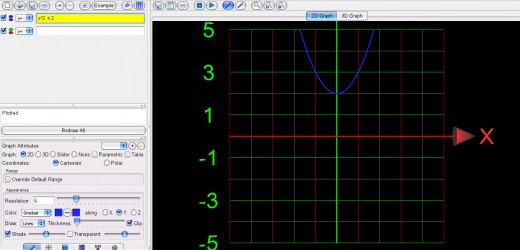
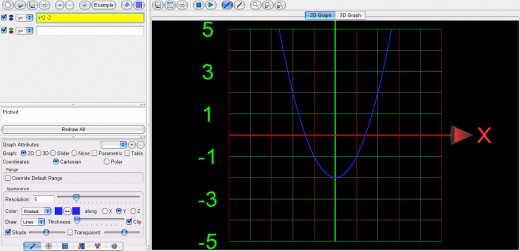
Below are the graphs of y=x2 , y=x2 + 2,y=x2 - 2.
y=x^2
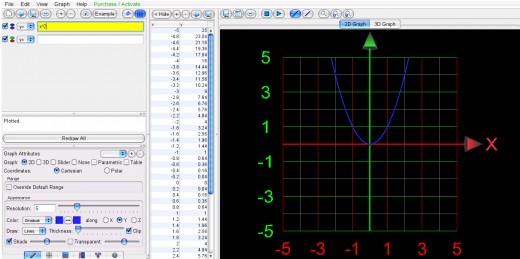
y=x^2 + 2
y=x^2 - 2
Check your understanding
view quiz statisticsSince explaining all the types in a single article would make it much lengthy, therefore, the remaining types would be discussed in the next articles. These articles are being written keeping in view that many of us don't have the basic knowledge about these things. So this would be much easier for most of you guys. However the next articles would contain something new for most of you guys. Solve the short quiz in order to check your understanding.
In case of any confusion comment below.