Elements of Mass; Vector and Spin

When an organized mass is in rotation, the angular momentum generated about as spin axis creates a perpendicular inertia in conjunction with the angular momentum. This perpendicular inertia is only observed when the rotating mass is rotated at right angles to the vector of the spin rotation. The whole rotating mass can be moved in any direction easily, subject to the laws of linear inertia and momentum, as long as it is not rotated in an angle other than the spin vector. This curious fact demonstrates that momentum and inertia are also bound together in an angular relationship similar to that found between the electric force and the magnetic field. In an electric flow moving along a wire, a magnetic field is generated at right angles to the vector flow of electrons. Conversely, a moving magnetic field will generate and electrical flow under the right conditions perpendicular to the vector direction of the magnetic field. A similar condition exists within an isotopic rotating mass with momentum and inertial vectors. It may be that mass itself acquires its characteristics from these facts. We can tease out certain peculiar aspects of mass under specific conditions.

A rotating spherical or planer mass contains angular momentum around the spin axis that is greatest at the equator and least at the poles and the center of the spin axis. Conversely, the rotational inertia generated by isotopic spin is greatest parallel to the spin axis and least perpendicular to it. All rest mass or mass in linear momentum have distinct types of inertia, so the isotopic inertia is directly related to the angular momentum of the isotopic spin. The isotopic inertia is in addition to the rest mass or that inertia related to the linear momentum. There are thus three distinct types of inertia. These can exist individually or in complex combination with one another. The complex combination of two or more is the usual state that exists for a mass.

The inertia related to angular momentum is used in inertial guidance systems. These consist of motor driven rapidly spinning gyroscope of some kind. But the phenomenon is not restricted just to gyroscopes. It exists throughout the cosmos. It is the force the keeps planets on a particular orientation with respect to a frame of reference like the stellar and planetary surroundings. The force can be altered only with the application of an external force according to;

F = MA (1)

Where mass M is involved with the 1^st derivative of velocity A (acceleration) to produce the product, the force F. When the velocity, and thus acceleration is confined to an isotopic spin, then inertia becomes directed perpendicular and tangent to the vector momentum of the isotopic spin. Only when the rotating mass is forced to change in vector orientation other than the vector of spin, does this type of inertia become apparent.

Keep in mind that both velocity and acceleration are vectors that have a discrete modulus and scalar (direction and size roughly speaking). With the relationship between virtual and real particles, mass too acquires a vector relationship and thus has vector qualities. It is the secret between the false and real vacuums that causes mass to exist in the first place, that things like inertia and momentum can exist at all in relation to vector mass.

This has implications for the understanding of the cosmos on a deeper level and can be used, as it is partly today, to create phenomena from these obscure causes.

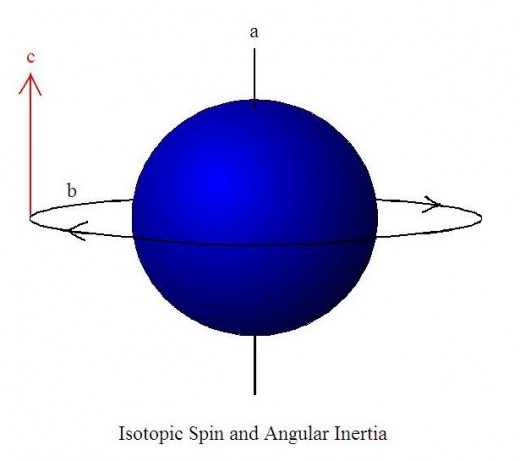
Consider the diagram above of a rotating spherical body. Broken into constituent parts we have the spin axis a, the spin direction b, and the tangential direction of the spin inertia c. This is as stated, in addition to the rest mass, or momentum mass of the body in linear motion. All elements are relative to one another, each acting as a frame of reference for the others. In the case of a spinning disk, the inertial force described in direction c, is concentrated as the mass is concentrated in a planar disk about the equator or region of maximum effect. We have a clear-cut case of inertia c being perpendicular to angular momentum b. We can call this effect angular inertia. It does not matter in which direction the body is rotating. The resultant angular inertia will still be in the same relationship with the spin direction and the rotational axis. A peculiar quality exists with this inertia is that it will not convert to momentum when and external force is applied. Once the force is removed, the rotating body will remain in a new orientation without further deviation. Here we have the principle of the non-conversion of inertia to momentum. Inertia in this case predominates and momentum will only occur as long as an overwhelming force is applied and no longer. Once the force is removed, then the inertia reasserts itself. This is not the case with linear momentum. A force applied to an inert mass will induce momentum in the vector relation with the force and once the force is removed, the mass remains in momentum. This is also true for angular momentum.

On the quantum level, angular momentum is quantized and one can measure either the scalar or the modulus, not both due to the prohibition of the uncertainty principle. Particles can have an intrinsic spin angular momentum as well as an orbital angular momentum.

Most planets and stars tend toward being spherical, with only a slight displacement of mass toward the equator due to rotation. In addition, there are a multitude of influences that act upon the bulge to cause precessional or processional wobble. In the case of the Earth-Moon system, the Moon’s orbit inclined the Earth’s equatorial plane, is the driving force for precessional wobble. Precessional wobble always moves in the same direction as the spin. Indeed, when a gyroscope or toy top is spinning at high velocity, these too will tend to wobble for the same reasons. This may be corrected by cancelling out the wobble by coupling two oppositely rotating objects. Though experiments show that this is so, they also demonstrate that mass of spin also cancels, demonstrating the peculiar ephemeral quality of mass. You can rig an experiment or watch the video on this phenomenon. In one stroke, the concept of positive and negative relative mass is proven. Two oppositely spinning gyroscopes that are physically linked will cancel the gyroscopic force, no matter if the gyroscopes are linked axis to axis (over/under) or side by side, as long as the two axes are parallel. On the other hand, if both gyroscopes have the same direction of rotation, their combined force is enhanced. Operating in tandem, the precessional force is eliminated to a large extent. This is a key finding suggesting why an ordinary lump of matter does not have vector mass of its own, because the isotopic spin of each part is in random orientation to the rest. On a large scale, the individual forces combine and cancel. On the surface, there appears to be no reason to think that the opposite rotations will cancel out the angular inertia by destructive interference such as one would find in electromagnetic phenomena, self-interference or in a Bose-Einstein condensate, but experiment proves the counterintuitive point., What remains is to determine the nature and extent of physical contact.

In the matter of extremely large spinning disks, i.e., galaxies, we often see spiral patterns present. This can be understood when relativistic frame dragging effects are taken into account. Of course, large spirals also exhibit mass polarization.

A single rotating magnetic disk can be made to levitate within a gravity well due partly to the angular inertia. Other reasons for levitation are the presence of an ambient magnetic field in which the disk is spinning; an existing and created magnetic turbulence in general. At extreme rotational velocities, a phenomenon known as magnetic field collimation occurs. This is part of the principle behind the Levitron. In the right conditions, the principle physics of the Levitron can be scaled up.

Consider an ordinary lump of matter. It consists of many atoms and quantum parts. These are often thought as spinning, proof of this is when particle accelerators smash atoms and the parts go spiraling in myriad directions in a magnetic field. The reason we don’t have much in the way of much perpendicular directional inertia in such a lump, is due to the fact that the constituent quantum parts are arranged in a random orientation. Directional inertia is thus expressed toward all vectors. One can simply test this idea by picking up a large mass and then turning on one spot while holding the mass. You will notice a resistance to move as you begin the turn. You will also notice a resistance to stop when you stop turning. Here we see coupled angular momentum and inertia in action.

The question of the day now is, if we somehow collimate the quantum parts to a parallel alignment, can we see a specific directional inertia being expressed without spinning the whole lump? A thought experiment is suggested consisting of a multitude of small gyroscopes in two arrangements, i.e., where the spin axes or randomly oriented and where they are all parallel and with the same rotational vector. The answer to the second half of the thought experiment comes from an actual experiment where two gyroscopes are coupled with axes parallel, but spinning in opposite vectors. There is no directional inertia here, so by projecting to a multitude of gyroscopes, we can say that the case will hold. Only if they all have the same direction of spin, will directional inertia hold. Take the experiment a step further. Just as in orienting the spin axes so that they are parallel, we can have the spin uniform in one direction, or half and half, where spin orientation faces in opposite directions. In the quantum world, uniform spin orientation results in the generation of a magnetic field. In the quantum scale, spin does not mean the same thing as at our level of experience. This is a complex issue debated by many physicists and it must be dealt with as an issue in its own right. Does this then suggest that magnetism, especially in the form of a permanent magnet, is related to perpendicular mass, particularly at the quantum level? As all things in the cosmos are interrelated, the answer is yes. But the quantum realm is a peculiar place, where the magnetic force is not directly related to directional mass, i.e., non magnetized mass.

The first part of the thought experiment with random orientations is also answered. A large mass will have an inertia of rotation in any vector as well as an inertia related to linear vector. This then is why it is difficult to start a large mass rotating in any vector, and once rotating, difficult to stop it. However, in the case of a spinning gyroscope or planet, the perpendicular inertia generated by the rotation is a peculiar type of inertia that does not readily convert to angular momentum. Angular momentum is concentrated in the plane of spin, perpendicular to the spin axis. The inertia generated by the spin prevents angular momentum from occurring when we rotate the spinning mass toward the axis. We can move it with force, but once the force stops, so does the rotation toward the spin axis. This curious fact is easily done with gyroscope experimentation. Force cannot generate a sustained angular momentum perpendicular to the spin angular momentum if that force is not continuous or is stopped. What is changing in one vector, i.e., the direction of spin and the angular momentum affixed thereto, is fixed in the perpendicular vector.

We know that matter and energy are interchangeable as expressed in general relativity and we have gone on to experimentally prove this fact. We know that this exchange occurs in discrete quantum amounts. One of the classic conversions is seen in the change of an electron-positron pair into two energetic photons when the electron-positron annihilate on contact with one another. We also know that the process is reversible and that the two photons can also come from a pion. Matter and energy exhibit both particle and wave characteristics. If we can take two photons from a pion, that generates them as polarized and entangled entities, can we then cause the photons to collide and create a polarized electron-positron pair? If we could, we may be able to create polarized mass and thus concentrate mass vector expression along a specific orientation.

Just as we can make entangled self-interference with a double slit for single photons, we can now do with a bunch of atoms in the form of a Bose-Einstein condensate. The ramifications of this are immense. Some paradigm altering results are coming from new experiments. In some circumstances, we can either collimate or arrange photons in a polarized array. It follows that with an atom laser that runs on a Bose-Einstein condensate, that we should be able to collimate and polarize matter as well under these conditions. If matter can be polarized, then we should be able to detect right angled inertial and momentum qualities. In a limited way, this has already been accomplished with experiments investigating the Casimer effect. Two corrugated and very tiny gold plates were induced to move sideways under the effect of a force perpendicular to the plane of the plates. If right angled inertia can be harnessed, the implications are enormous.

Experiment # 1 involves spinning a gyroscope in one direction i.e., counterclockwise and then spinning it in the opposite direction. You will find that the wobble that occurs in the spinning gyroscope tends to occur in the same direction as the spin. In other words, a counterclockwise spin will be coupled with a counterclockwise wobble and a clockwise spin will be coupled with clockwise wobble. This leads to the next experimental concept.

Experiment # 2 is three separate exercises involving to oppositely and similarly spinning gyroscopes, counterclockwise and clockwise, fixed together end to end and connected along the spin axis or parallel to each others spin axes, side by side, so that the axes of the two point in the same vector. Each gyroscope is set to spin in opposite rotation and the results of that experiment recorded. The hypothesis is that there will be reduced or no wobble and no effect on stability. The results of actual experiments demonstrate that both wobble and vector inertia is cancelled with oppositely spinning gyroscopes. With similarly spinning gyroscopes, wobble is cancelled but directional inertia is enhanced. This holds for a. Gyroscopes mounted over/under, b. Gyroscopes linked and mounted side by side with axes parallel and c. For gyroscopes in opposite or similar spin but unconnected. In the last case, wobble remains.

Experiment # 3 involves a levitated mass, either a magnet of known rest mass in the Earth’s gravity, or the same magnet or a measured like mass in a zero G environment. The mass is fired at 9.81 Ft/sec and measured at the test end by an impact sensor for the instantaneous mass of acceleration when it is stopped dead in its motion. From this we can learn a lot, as we know that mass varies as the square of the velocity. The mass can be fired at different velocities to build a statistical record. The hypothesis here is that mass is a vector with both scalar and modulous and is relative. Stage one of the experiment will have the mass resting on the sensor plate without motion. The result should be zero or a vanishingly small mass. The second stage will be to fire the mass at measured velocity with the apparatus oriented in differing vectors, hence the desirability of a zero G environment. The measuring apparatus is to consist of a timer, a mass sensing apparatus, a clock start and clock stop laser triggers at the ends of the run. In addition, there is a distance measuring tool. All of this can be integrated with a computer.

LAWS of MASS

Until now, scientists did not define mass beyond a fundamental unit for calculating more complex phenomenon. An investigation using observations and experiments can help us define mass and give us a deeper understanding of the cosmos. Experiments can clarify what mass is and how it functions. Observation of experiments and of nature, can give more clarity. Finally, putting this together can give us a theory of mass. Form observations and experiments we can find the following.

1.      Mass is relative, conforming to the constraints of General Relativity (GR), in all its aspects, such as frames of reference, Lorentz transformations and so forth.

2.      Mass only exists when matter is in motion. Matter is always in motion of one kind or another, relative of each and every piece of matter to all other pieces of matter. Matter exists in a quantum state on the subatomic level and motion is affected via discrete jumps through a feedback process between virtual and real matter. Thus mass is also subject to quantum discreteness and created by quantum processes. Considering that matter and energy are interchangeable, energy also contains mass, and this can be demonstrated in the photoelectric effect.

3.      Mass can form in a particular vector both in scale and direction. This is affected in two ways. Mass tends to concentrate in the direction of travel and in rotating bodies, is perpendicular to the direction of rotation. In the latter case, it can be said the mass can be polarized. It is generated perpendicular to the direction of angular momentum. In the case of vector mass, depending on the frame of reference, mass can measured in positive, zero or vanishingly small and negative values.

4.      There is a mass of inertia and a mass of momentum (both linear and angular). Under certain conditions, the inertial part can be perpendicular to the momentum part of mass. This establishes a similarity to other perpendicular arrangements like electrical and magnetic phenomenon.

5.      Vector mass increases in square to the vector velocity of motion during linear momentum in relation to the frame of reference in which it is in relative motion. Logic would say that this is also true for polarized mass, but this is hard to measure. Polarized mass results from spin and mass is greatest parallel to the spin axis. This mass can be measured when one attempts to rotate spinning mass perpendicular to the direction of spin. As spin is very vector specific, any rotation toward the axis of spin, is perpendicular to the spin vector.

6.      Rest matter has mass called rest mass because all of its constituent quantum parts are all in motion. If the constituent parts can be aligned, mass could also be aligned. Rest mass can only be measured in relation to a mass in motion near it. However, one piece will interact with another, so mass can only be inferred by the perturbation interaction of both pieces and the amount of perturbation that is usually unequally divided between the pieces.

7.      There is a mass of gravity and a mass of acceleration as Einstein proved the equivalence of gravity and acceleration.

8.      Growing evidence suggests that mass only exists due to other mass. As the cosmos is made up of countless pieces of discrete mass all acting on one another in many ways, individual pieces acquire inertia and momentum accordingly, within the constraints of GR. Each piece of mass affects all other pieces in the cosmos and vice versa. Many pieces in orbit around a large central mass, will sort into a discrete banded accretion ring according to harmonic orbital period resonance in a complex manner. This serves as part of the proof and no where is this better seen than in the discrete ring structure of Saturn.

9.      Mass and energy are interchangeable according to E = Mc². It is known that energy has mass, as in the photoelectric effect, a fundamental principle of quantum physics. Matter and energy are two aspects of the same thing. Mass is involved with matter and energy. Mass is intrinsically tied up with matter, but not exclusively so.

10.  Two equal masses remain equal provided that their relative velocity is the same and/or gravitation upon them is identical.

11.  Einstein stated that mass tells space/time how to curve and space/time tells mass how to behave in space/time. This is a complex feedback loop.

12.  Mass behaves in a discrete quantum manner, subject to the Planck length and Planck moment. The concept of dark matter and dark energy (invisible to our means of detection) is born out by observation of the cosmos and is related to virtual particles/energy manifesting out of the false vacuum state. The interaction of the Planck vacuum with quantum matter creates mass. As visible matter and energy remains constant in an expanding cosmos, the proportion of dark matter and dark energy increases in relation to the visible because the constant of dark matter and energy is the Planck moment and Planck length. The increase of space allows more virtual particles to form over all in that expanding context.

13.  Infinite mass implies an infinite cosmos and zero mass implies no cosmos. The observed truth lies somewhere in between zero and infinity and our understanding must follow observed nature. At the moment of the big bang, mass was virtually infinite and space was virtually zero. As the cosmos expands under acceleration, mass will approach zero and space will become virtually infinite.

Why precession? Precession occurs due to two factors. One is due to unevenness in the spinning mass. The larger the mass, the more uneven it is. Consider the Earth. The gravity field of the Earth is uneven due to the mass distribution and dynamical changes in the whole. This was discovered in the early days of NASA satellite tracking when satellites were lost primarily over the Indian Ocean. The second reason is due to perturbation. Once more referring to the Earth, the two agents that perturb the Earth the most are the Moon and Sun. Due to the Earth’s inclination to the ecliptic, and the Moon’s orbital plane that is inclined to the Earth’s equatorial plane, both the Moon and Sun act on the equatorial bulge of the Earth to cause wobbling and precession.

Some precessional influences can even cause planetary instabilities where the axis of spin can alter radically and suddenly in orientation. This is more true of slow spinning plants like Venus and Mercury and less true for rapidly spinning planets like Jupiter and Saturn. Considering the foregoing experiments, particularly the second set of experiments, there are interesting implications about planetary relationships. The one major question that remains is what exactly constitutes physical linkage/contact. Can physical linkage be achieved through gravity and or magnetism alone between physically separated bodies? If the magnetic, gravitational or even harmonic linkage has an effect, then Venus’ retrograde rotation could affect Earth, which rotates prograde. The interaction of Venus and Earth might cause instabilities in both planets beyond just orbital ones. Then there is relative rotation of one body compared to another as in between the moon and Earth as well as the moon’s orbital period in relation to the Earth’s spin. There are many deep considerations that arise out of experiments involving two or more rotating bodies.

Another consideration is about the spin mass of the cosmos as a whole and if this can be detected and used to probe the nature and extent of it beyond what we already know. The individual parts are in rotation on all levels and in an apparently random distribution over all..

As we know that mass is polarized, we can put it to use. One current use is in inertial guidance systems. There are no doubt other uses to be developed. By understanding what mass really is, we open the doors to new and interesting possibilities.