Electrical Frequencies, Conversions with Other Measurements

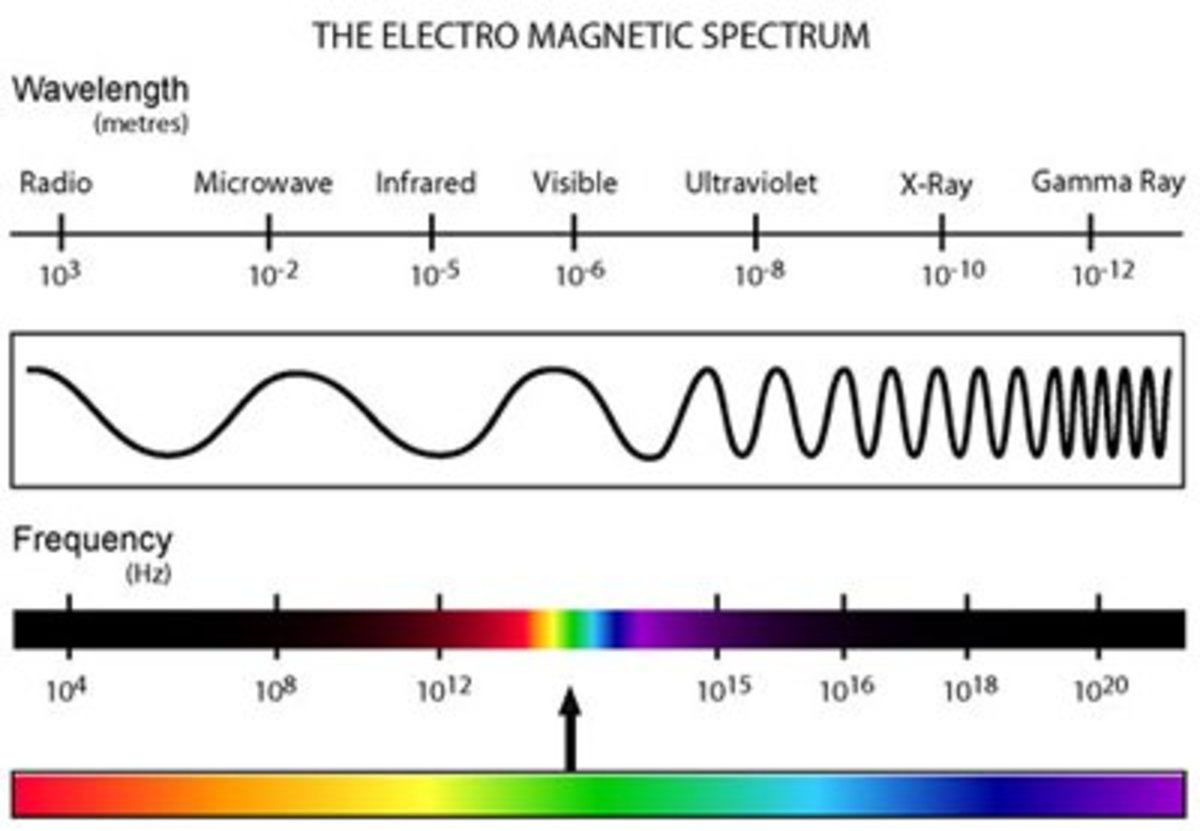
Frequency is defined as the number of times a cycle repeats itself over a specified period of time. In the case of sound, frequency is measured in Hertz (Hz). One Hz moves at 1 cycle per second. Calculating sound intensity requires measurements of the sound wave height (known as amplitude) which is recorded in in decibels (dB). Frequency can be converted from the speed of sound (Hertz, Hz) to wavelength (defined as the speed of light in a given period of time), into angular velocity (defined as angular displacement in a given period of time), or into rotational speed (defined as the number of rotations in a given period of time).

Hertz Math

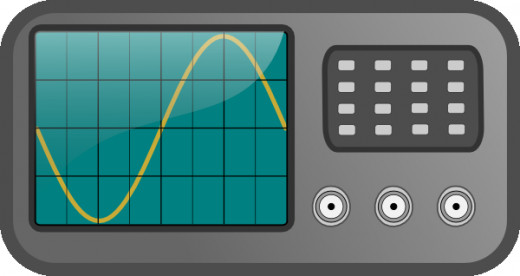
One way to witness sound waves in action is to view them on an oscilloscope screen. After turning on the oscilloscope, a line appears on the screen. Attaching a microphone to the oscilloscope allows several different types of sounds to be inputted into the device. The sounds produced will cause the line on the screen to jump up and down in a wave formation. To use an oscilloscope, play a sound for 15 seconds while counting the number of waves it produces. At the end of the 15 seconds, divide the number of waves by 15 to obtain the Hertz, or cycles per second.

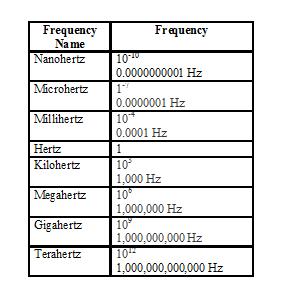
Play the sound again to measure the wave height. Each sound produces its own amplitude (the measurement of the wave height) and frequency (the distance between wave peaks). One Hertz (1 Hz) equals 1 wave cycle per second. But these wave frequencies have multiples and fractions with their own names (as seen in the table below). For example: 1,000 waves per second equals 1 kilohertz (kHz) and nanohertz is the equivalent of 10^-10 Hz which is a sound wave that that travels at a speed of 0.0000000001 Hz per second.

Angular Velocity and Rotational Speed Calculations

Angular velocity is measured in radians per minute and the conversion equation is: 1 Hertz = 376.99 radians per minute. First the Hertz must be converted from cycles per second to cycles per minute, then multiplied by the radians per minute. So 1,000 Hz (1,000 cycles per second) = 1,000 x 60 (60 seconds per minute) = 60,000 cycles per minute x 376.99 radians per minute = 22,619,400 radians per minute. So 1 kilohertz (1,000 Hz) is equal to 22,619,400 radians per minute.

Rotational speed is measured in revolutions per minute (used to measure engine speed and torque). As with angular velocity, the Hertz measurement must first be converted from cycles per second to cycles per minute before multiplying it by the revolutions per minute (RPM). In this case, 1 Hz is equal to 60 revolutions per minute (RPMs). So, 1 kilohertz = 1,000 cycles per second x 60 seconds = 60,000 cycles per minute x 60 RPMs = 3,600,000; 1 kilohertz is equivalent cycles at a speed of 3,600,000 revolutions per minute.

Frequency and Wavelength Conversions

The speed of sound (measured in frequency) can be compared to the speed of light (wavelength) by knowing the following facts:

• · 1 Hertz (sound) travels at 1 cycle per second
• · 1 Wavelength (light) travels at 299,792,452 meters per second - which is known as the speed of light.

So to convert a Hertz frequency reading to a light wavelength reading, divide the frequency by the wavelength. This produces the following calculations:

• · 1 Wavelength = 299792.458 Gigahertz
• · 1 Gigahertz = 299792.458 Wavelengths.

References

Wikipedia. Hertz.

http://en.wikipedia.org/wiki/Hertz

Convert World: Frequency

http://www.convertworld.com/en/frequency/

Ask Numbers: Frequency Conversion

http://www.asknumbers.com/FrequencyConversion.aspx

Zyra: The Relationship Between Frequency and Wavelength

http://www.zyra.org.uk/freqwav.htm

Time and Frequency Division, National Institute Standards and Technology: Time and Frequency From A to Z

http://tf.nist.gov/general/enc-f.htm

Convert Units: Convert RPM to Hertz

http://www.convertunits.com/from/RPM/to/hertz

Elliot, Rod. Elliot Sound Products: Frequency, Amplitude and dB.

http://sound.westhost.com/articles/fadb.htm

Brigham Young University: Frequency, Wavelength, Energy Calculator

http://www.photonics.byu.edu/fwnomograph.phtml

Berkley: Hertz

http://ptolemy.eecs.berkeley.edu/eecs20/sidebars/hertz/