Differentiation using the quotient rule formula. How to differentiate an algebraic fraction.

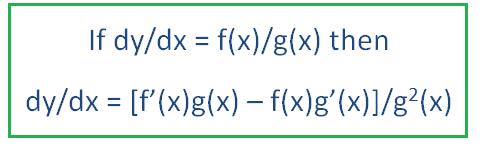
The quotient rule can be used to differentiate an equation when you have one function being divided by another function. All you need to do is look for an algebraic fraction (a function of a x on the numerator and a function of x on the denominator).

So if your equation y takes the form y = f(x)/g(x),

then dy/dx = [f’(x)g(x) – f(x)g’(x)]/g²(x)

Let’s go over some examples that involve the quotient rule.

Example 1

Use the quotient rule to differentiate y = 7x³/cos3x

As you can see you have an algebraic fraction is it is clearly a quotient rule question.

First of all write down the functions f(x) and g(x):

f(x) = 7x³ and g(x) = cos3x

Next work out the derivatives of these two functions:

f’(x) = 21x² and g’(x) = -3sin3x

All you need to do next is substitute these into the quotient rule formula:

dy/dx = [f’(x)g(x) – f(x)g’(x)]/g²(x)

dy/dx = [(21x²)(cos3x) – (7x³)(-3sin3x)]/(cos3x)²

All you need to do next is tidy up this derivative:

dy/dx = [21x²cos3x + 21x³sin3x]/cos²3x]

Example 2

Use the quotient rule to differentiate y = e^4x+1/sinx

Again you have an algebraic fraction so use the quotient rule:

First of all write down the functions f(x) and g(x):

f(x) = e^4x+1 and g(x) = sinx

Next work out the derivatives of these two functions:

f’(x) = 4e^4x+1 and g’(x) = cosx

All you need to do next is substitute these into the quotient rule formula:

dy/dx = [f’(x)g(x) – f(x)g’(x)]/g²(x)

dy/dx = [(4e^4x+1)( sinx) – (e^4x+1)(cosx)]/(sinx)²

All you need to do next is tidy up this derivative:

dy/dx = [4e^4x+1.sinx - e^4x+1.cosx]/sin²x]

You can also factorise the top and divide the numerator and dive the numerator and denominator by sinx:

dy/dx = [e^4x+1(4-cotx)]/sinx

Let’s take a look at one last example that involves using the quotient rule.

Example 3

Use the quotient rule to differentiate y = ln(7x+4)/(5x²+3)

Again you have one function of x dividing another function x so the quotient rule can be applied to this question:

First of all write down the functions f(x) and g(x):

f(x) = ln(7x+4) and g(x) = 5x²+3

Next work out the derivatives of these two functions:

f’(x) = 7/(7x+4) and g’(x) = 10x

All you need to do next is substitute these into the quotient rule formula:

dy/dx = [f’(x)g(x) – f(x)g’(x)]/g²(x)

dy/dx = [(7/(7x+4)).(5x²+3) – (ln(7x+4).10x]/(5x+3)²

All you need to do next is tidy up this derivative:

dy/dx = [(35x²+21)/(7x+4)-10x.ln(7x+4)]/(5x+3)²

Summary

So as you can see from the last 3 examples the quotient rule can be applied when you have one function being divided by another function. If this is the case, then write down formulas for f(x), g(x), f’(x) and g’(x) and then substitute these into the formula dy/dx = [f’(x)g(x) – f(x)g’(x)]/g²(x). Be careful when simplifying your answer and use plenty of brackets to help you distinguish between the different functions.