Fun with Powers of Two
Fun with Powers of Two
Powers of 2 make the world go 'round. Math doesn't have to be calculus and algebra. A little exposure to all things divisible by 2 can't hurt, can it?
Binary Numbers are built from powers of two
Binary numbers are written such that all the digits represent powers of two. Computer scientists and engineers quite often do their work in binary. By contrast, decimal numbers are written such that all digits represent a power of 10. We all learn decimal numbers in school, starting from day 1 in kindergarten.
We only need 2 digits
Because we typically come with 10 fingers, humans prefer base 10 numbers. We need 10 digits to represent every possible positive integer value. On the other hand (so to speak) base 2 numbers require only 2 digits. We can select any two symbols for those two digits, but we typically employ combinations of zeroes and ones.
How does binary a number appear?
A positive binary integer is a sequence of zeroes and ones. Every sequence represents a unique numerical value (ignoring leading zeroes). For our examples we will use 4 digit numbers. We could pick any number of digits, but 4 is manageable for human brains and it also dovetails with many computer science applications.
For example, consider an arbitrary 4 digit number:
10102
We write the number with an optional '2' subscript to distinguish it from a base 10 number. The subscript isn't obligatory; if an equation or a document contains numbers of only one base, then the subscript may be omitted. It's a judgment call. Sometimes it simply gets in the way and becomes distracting.
Let's convert our base 2 number (above) to base 10.
(1 * 23 ) + (0 * 22 ) + (1 * 21 ) + (0 * 20)
Adding up the terms, we get:
8 + 0 + 2 + 0 = 10
The base 10 equivalent of 10102 is 1010.
Getting slightly more specific, each digit is assigned an index number, starting with the rightmost digit being assigned the number 0. Believe it or not, base 10 numbers are broken down in precisely the same style, but we have been trained to do it in our heads. Anyway, since our previous example has 4 digits, the rightmost digit is assigned the number 0. The leftmost digit will be referred to as digit number 3. If you don't mind counting from zero, it's not that bad, right?
Here's the trick: the index numbers we discussed in the previous paragraph correspond to powers of 2. The rightmost digit, to which we assigned the index value '0', is the placeholder 20. The leftmost digit is the placeholder for 23. All we have to do in order to convert to base 10 is calculate the powers of 2 (based on the index number) and add up those powers if the corresponding digit is a 1. If the correspondence digit is a 0, we can ignore it.
Fun with Powers of 2 in the real world
We can identify examples of base 2 numbers in the real world. Does this look familiar?
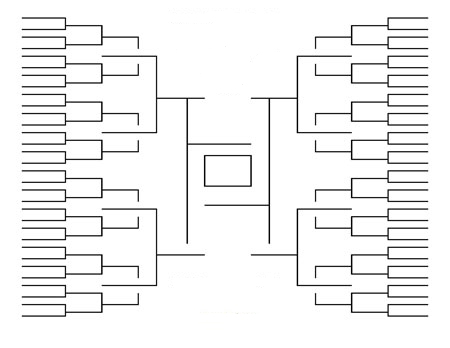
Didja ever wonder?
It's the NCAA Men's Basketball Tournament bracket. Have you ever pondered why they invite 64 teams? Why not 60 or 70? 64 is a (somewhat) magic number because it's a power of 2. It's 26. Each time a 'round' of games is completed, the number of teams decreases by 1/2. If we started with 60 teams, we'd follow this sequence:
- Round 1: 60 / 2 = 30
- Round 2: 30 / 2 = 15
- Round 3 ... uh oh.
Note that round three presents a problem because the pool of 15 teams left over from round 2 is clunky. We can create 7 pairings with one team left over. Does that team move on to the next round or does it get sent home? No one's happy, except the sports-talk radio shows.
By starting with a team count that's a power of 2, we are guaranteed a smooth transition to a championship game:
- Round 1: 64 / 2 = 32
- Round 2: 32 / 2 =16
- Round 3: 16 / 2 = 8
- Round 4: 8 / 2 = 4
- Round 5: 4 / 2 = 2
- Round 6: 2 / 2 = 1 (One team is left standing. A champion is crowned.)
Should the tournament modeled above wish to expand, their options are limited. Were a computer scientists in charge of expansion, the obvious choice would be to multiply the current number of teams by 2, thereby creating a larger pool that is still a power of two. The tournament would jump from 64 to 128 teams. Round 1 becomes 64 games instead of 32; 1/2 the teams are eliminated. If 128 teams is too many, then any other alternative creates a scenario under which all the teams won't play in the first round. The sports world calls this a 'bye', or a free pass.
If you've ever filled out an NCAA bracket, you have some idea how many possibilities must be considered. Along with all the teams, powers of 2 also play a big part in the calculations. Let's start with the total number of games: through 6 rounds we have 32+16+8+4+2+1 = 63. We see that 63 games are required to eliminate 63 teams and give us tournament champion. How many different brackets would need to be filled out in order to account for every possible combination?
263 = 9,223,372,036,854,775,808 (9 quintillion)
We can confidently assert that filling out 263 brackets will guarantee a winner. That's a lot of clicking. If you're a basketball fan, you might know that no #16 seed has ever beaten a #1 seed in the first round of the tournament. Given that the bracket has 4 #1 seeds, we could eliminate those four games from our calculations with a high level of confidence. Each game that we remove reduces the total number of possible outcomes by a factor of 2.
259 = 576,460,752,303,423,488 (5 quadrillion )
Flipping a coin
Any process that produces two equally probable results can easily be described with powers of two. Think about flipping a coin. Flipping it one time will produce one of two possible outcomes; heads or tails. Flipping it 100 times will .... hmmm....
Let's make up an equation to figure this out.
If one flip produces two possible outcomes, we can say
2flips = # of possible outcomes.
In other words, decide how many times you plan to flip, then raise 2 to that power. Considering our rather ambitious plan to flip 100 times:
2100 = 1,267,650,600,228,229,401,496,703,205,376.
The equation tells us that flipping a coin 100 times will produce different 2100 different outcomes.
Conclusion
Powers of 2 make the (computer) world go 'round.