Circle Geometry Circle Solutions 1 for GMAT
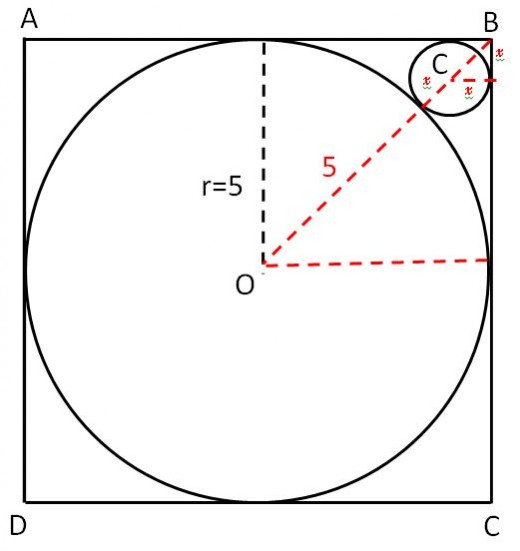
1
Let us name the radius of C centered small circle as X. BC is the hypotenus of the right triangle therefore hypotenus will be x√2. Same way for the O centered circle BO is the hypotenus and thelength is 5√2. We can create our equation from these information as following
5√2 = 5 + x + x√2
When solve the equation for x. you will find the x.
Correct choice is A
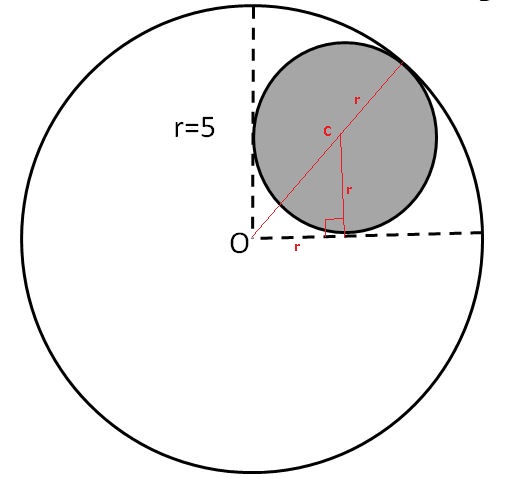
2.
If draw a line from center 0 passing through center C. It would be radius of big circle. It is goign to be equal to r*√2+r=5
If we resolved the equation we will get choice A.
Correct choice is A
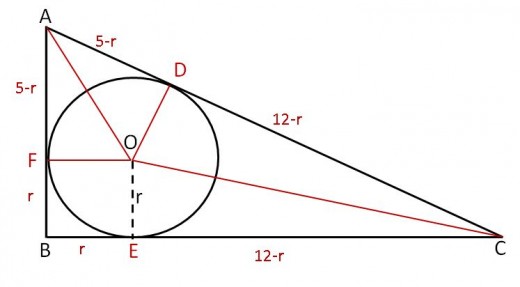
3.
when we draw those red lines. We can discover that AOF and AOD are congruent triangles. If r is the radius of the 0 centered circle then AF is 5-r. Since AOF is congruent to AOD triangle. AD is 5-r too. Same way OEC and ODC are congruent. CD is 12-r.
Since AC is 13 due to being hypotenus of the triangle. We can reach to following equation.
5-r+12-r = 13 when solve this equation we can find r = 2
Correct choice is D
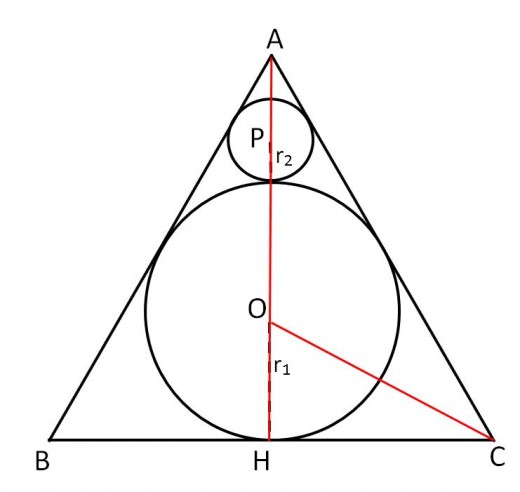
4.
If we draw a line from A to H, it will be the height of the equilateral triangle its length is 5√3
5√3 = 5 + r2 + r2√3
If we resolve this equation for r2 we get choice E
Correct choice is E
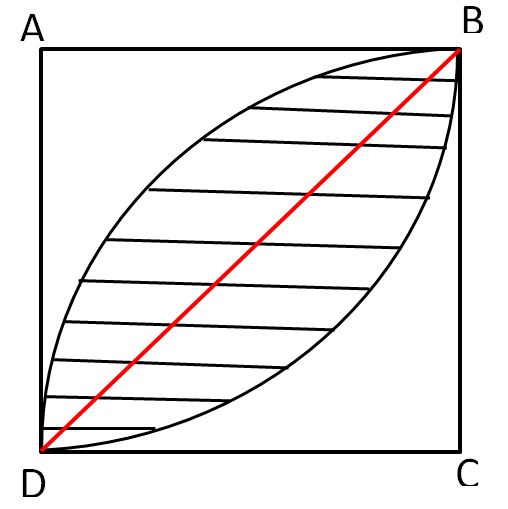
5
If we draw a diagonal line between B and D point, we would split the area into half. Now each side of that area is actually equal to a quarter of full circle minus ABD triangle area. Therefore;
Shaded area equals to 2*(0.25*Π*102-10*10*0.5) = 50Π - 100
Correct choice is C