Geometric number sequence help. What is the nth term formula for a geomtric sequence?

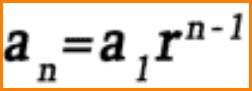
A geometric sequence is a sequence where previous term of a sequence is multiplied by a constant. This constant is called the common ratio (r) For example 2,10,50,250,1250... is a geometric sequence as the next term is generated by multiplying by 5 (common ratio = 5)

The nth term of a geometric sequence can be worked out quite easily. Let’s call the first number in the sequence a. Now to get subsequent terms in the sequence all you need to do is multiply the previous term by the common ratio (r). So:

the second term in the sequence will be ar.

the third term in the sequence will be ar².

the fourth term in the sequence will be ar³.

the fifth term in the sequence will be ar⁴.

Therefore the nth term of the sequence is ar^(n-1).

Example 1

Here is a geometric number sequence. Work out the nth term of the sequence.

4,12,36,108,324...

First work out the common ratio (r). This can be done by dividing two consecutive terms. Let’s choose the first two terms.

r = 12 ÷4 = 3

The first term of the sequence is 4, so a = 4.

All you need to do now is plug these two values into the nth term formula:

nth term = ar^(n-1)

nth term = 4.3^(n-1)

Example 2

Here is another geometric sequence. By calculating the nth term, work out the 20^th term in the number sequence.

0.04, 0.06, 0.09, 0.135, 0.2025...

Like the previous example, work out the common ratio by dividing the 2^nd term by the 1^st term.

r = 0.06 ÷ 0.04 = 1.5

Also, a = 0.04 (since the first term is 0.04)

Therefore, the nth term of this geometric number sequence is:

nth term = 0.04×1.5^(n-1)

Now all you need to do is plug in n = 20 to work out the 20^th term:

nth term = 0.04×1.5^(n-1)

nth term = 0.04×1.5^(20-1)

nth term = 0.04 × 1.5^19

= 88.7 to 3 significant figures.

Example 3

The 3^rd term of a geometric number sequence is 180 and the 4^th term is 1080. Work out the nth term.

This time you need to divide the 4^th and 3^rd terms together to get the common ratio.

r = 1080 ÷ 180 = 6

Now, you can use this to work out the first term in the sequence working backwards from the 3^rd term in the sequence.

2^nd term = 180 ÷ 6 = 30

1^st term = 30 ÷ 6 = 5

So a = 5.

Therefore the nth term is:

5×6^(n-1)