Grid Method of Multiplication
How to Learn to Multiply Using The Grid Method
When I was at school, I'm quite sure (it was a long time ago) that we learned our times tables. up to 12 x 12, and then progressed straight to learning the traditional method of long multiplication. My children, and I think most children in state education in the UK, still learn their times tables but are introduced to long multiplication by learning the "grid method".
At first I was skeptical about this new method. I thought it might introduce an unnecessary step and confuse children that were capable of learning the traditional method of long multiplication. Having seen my children use it, I now think it could be a useful way to give children the understanding and confidence to tackle long multiplication.
Advantages of the Grid Method
The grid method is a very logical, step by step method. It's highly visual and by drawing up the grid, you begin to understand the mechanics of how multiplication works. It's relatively easy to see what to do at each step. This is in contrast to the traditional method of long multiplication where, instead of using the grid to make things clear, you have to grasp the understanding in your head rather than working with a visual aid (the grid).
The method is best explained using an example. Here's a video (after the video there's a written step by step guide to follow):
Example Grid Method of Multiplication 16 x 23
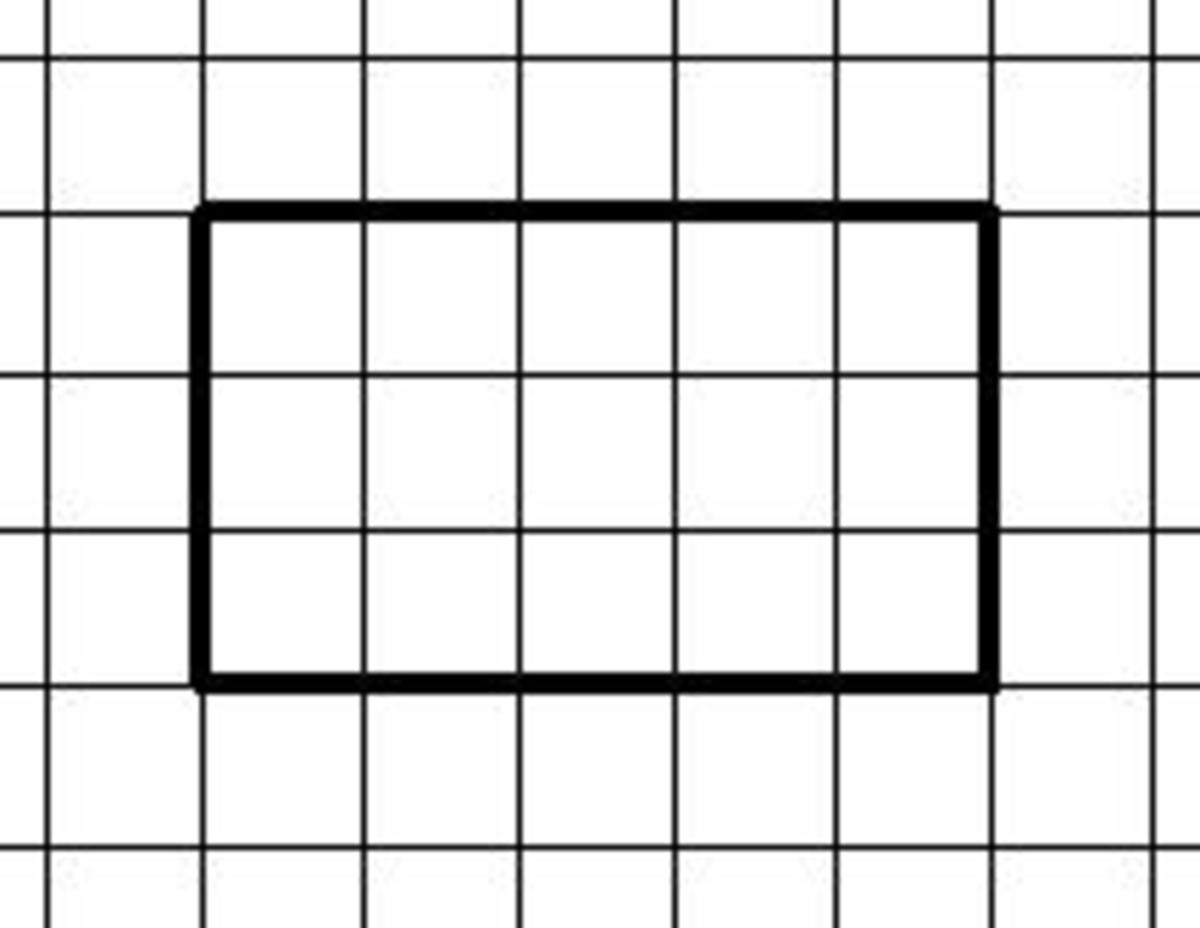
Example 16 x 23 Step 1 Draw up the Grid
We are multiplying 16 x 23 which is multiplying a two digit number by another two digit number. We need a two column by two row grid plus an extra header column and an extra header row and a total row. Here's the blank grid:-
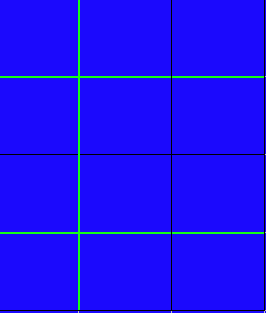
Step 2 Enter the Numbers into the Grid
Here we're multiplying 16 x 23. We need to break the numbers into tens and units. If they were three digit numbers they would need to be broken down into hundreds, tens and units. If they were four digit numbers then thousands, hundreds, tens and units.
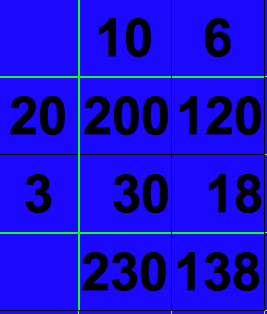
In this example 16 becomes ten and six. 23 becomes twenty and three. These are entered into the grid like this:

Step 3 Multiply Out The Grid
For each cell in the grid just multiply the first digits and add the number of zeros. That's hard to put into words so its best to just do it and it will become clear:
20 x 10 = 2 x 1 add on two zeros = 200
20 x 6 = 2 x 6 add on one zero = 120
3 x 10 = 3 x 1 add on one zero = 30
3 x 6 = 18
Then we just have to enter these numbers into the grid:
Multiply Out The Grid
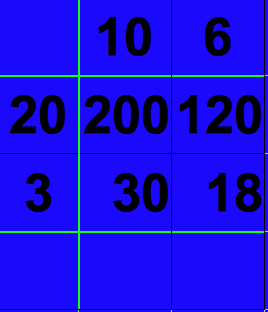
Step 4 Add up the Columns
In our example;
200 + 30 = 230
120 + 18 = 138
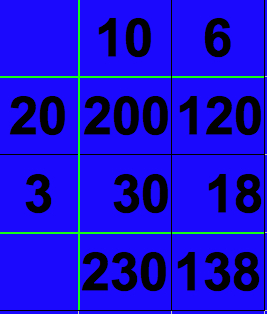
Step 5 Add the Totals
So we have 230 + 138 = 368 Final Answer
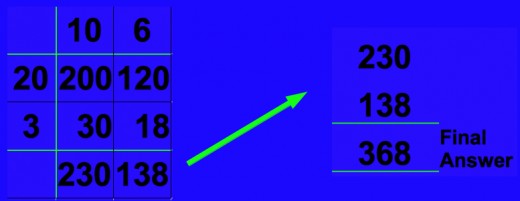
What do you think of the Grid Method of Multiplication?
Hopefully this has explained to parents how the grid method works and given children an introduction to multiplication using two or more digits. I'm convinced that this method is a useful stepping stone towards the traditional long multiplication method. You can also employ a simple technique to enable you to use the grid method for multiplying decimals. This will be covered in a separate hub.
What do you think of the Grid Method?