2019 GCSE Maths Calculator Paper, Key Grade 4 Topics
Predicting the topics that come up on the GCSE maths foundation calculator paper is much easier to do than for non-calculator paper. Here, I will go over some of the topics that are most likely to show up on this years’ maths calculator paper. Practice these topics well and you will be well on your way on obtaining a grade 4 in your GCSE maths exam.
1) Circles.
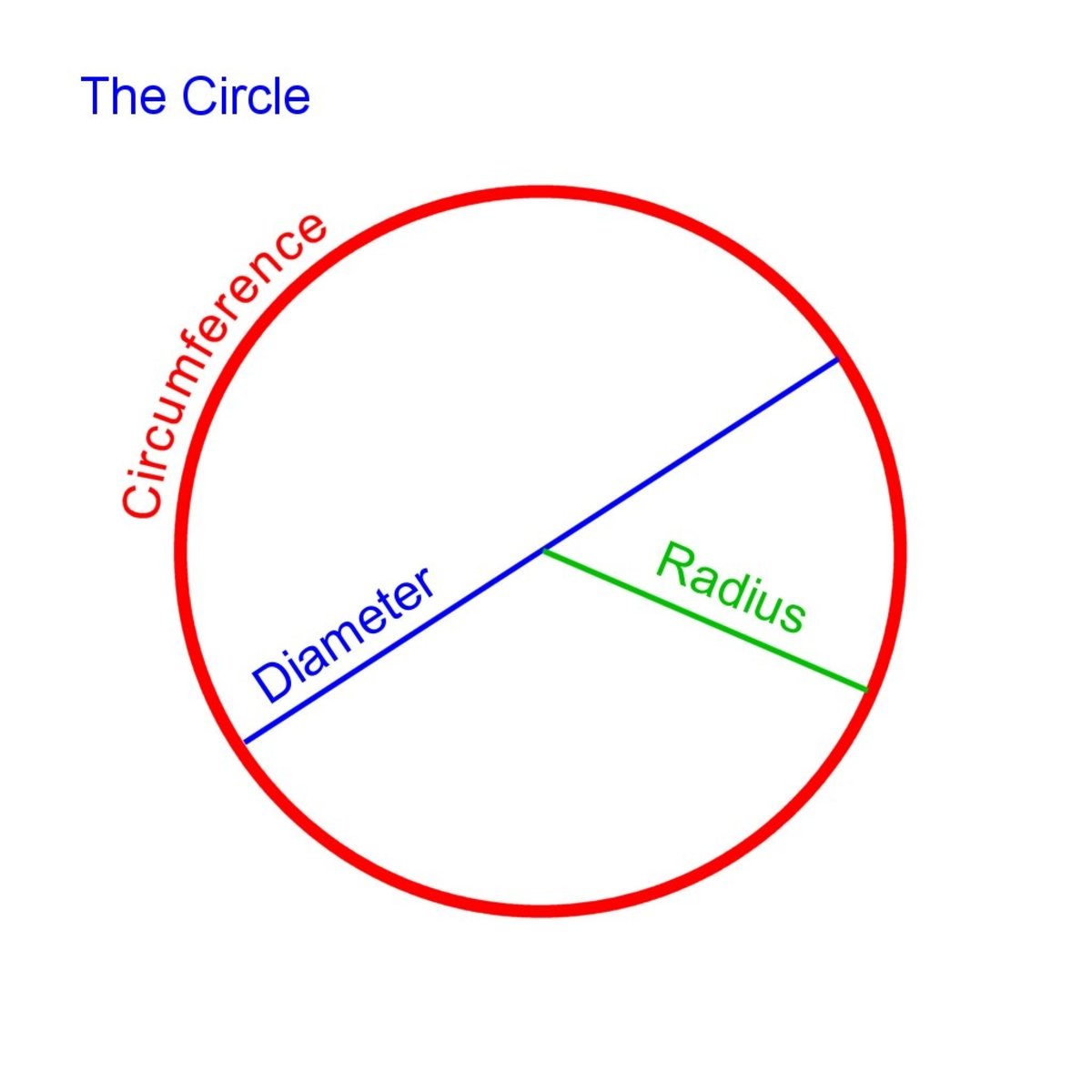
You will need to know how to calculate the area and circumference (perimeter) of a circle.
In order to calculate the circumference you need to multiply Pi (∏ = 3.14) by the diameter of the circle (C = ∏ × d)
Example
Calculate the circumference of a circle of diameter 9 cm.
All you need to do is substitute the diameter into the formula for circumference:
Circumference = ∏ × Diameter
C = ∏ × 9
C = 28.3 cm to 1 decimal place.
Finding the area is a little harder, as you need to work out the square of the radius, and multiply this by ∏ (A = ∏ × r²)
Example
Work out the area of the circle in the last example (diameter = 9 cm)
This time you need to use the radius of the circle. The radius is half the diameter (so r = 4.5)
A = ∏ × r²
A = ∏× 4.5²
A = 63.6 cm² rounded to 1 decimal place.
Harder questions on circles, may involve finding the area or perimeter of semicircles or quadrants.
For some more maths help on the area and circumference of a circle try these links:
How to calculate the area of circle giving your answer in terms of Pi.
Area of a semicircle. Finding the area of semi circles.
How to calculate the perimeter of a semicircle using 2 simple steps (semicircles)
2) Calculator usage questions.
You will expected to be able to work out squares (marked as x² on your calculator), cubes (marked by x³), square roots (marked with √)and cube roots (marked with ³√).
So to work out 2³, press the 2 key, followed by x³ key and then the ANS key. This should give you an answer of 8.
Also to work out higher powers, such as, 4⁷use the x⁰ key on your calculator.
Another typical question on the maths calculator paper, is when you have to divide a numerator of a fraction by the denominator of the fraction. You have to be very careful with the division sign.
Example
Work out this calculation to 1 decimal place.
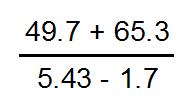
There are three ways you can do this calculation.
Method 1
Put brackets around the numerator and denominator and type this in on your calcualator:
(49.7+65.3)÷(5.43-1.7)
= 30.8
Method 2
Work out the numerator and denominator separately and then divide these two answers:
49.7+ 65.3 = 115
5.43 – 1.7 = 3.73
So 115 ÷ 3.73 = 30.8
Method 3
If you have a new calculator (natural display) then the full calculation can be typed in by hitting the fraction button key at the start of the calculation.
3) Trial and improvement
Trial and improvement is another typical question on the maths calculator paper. This is where you have to substitute the values of x into your equation to get a value that is close to the target number on the right hand side of the equation.
Example 1
Solve x² + 3x = 13 using trial and improvement, giving your answer to 1 decimal place. The solution lies between x = 2 and x =3.
Here the target number is 13, so you are looking the value of x which is closest to 13.
First substitute x=2 and x=3 into your equation. If this is done then you will lose method marks.
x=2, 2² + 3 × 2 = 10 (too small)
x= 3, 3² + 3 × 3 = 18 (too big)
Now go to your decimals as you know that the solution lies between x=2 and x=3.
x=2.5, 2.5² + 3 × 2.5 = 13.75 (to0 big)
x = 2.4, 2.4² + 3 × 2.4 = 12.96 (too small)
No more trials have to be done, as you only need the answer to 1 decimal place.
As you can see x = 2.4 is the best solution, as 12.96 is closest to 13.
For some more maths help on trial and improvement try reading this article:
4) Pythagoras
Make sure you know when to use Pythagoras is in your maths exam. Pythagoras is used on right angled triangles to find a missing side length if the other 2 sides of known. For quickness, you can follow these 3 steps:
1) Square the two given side lengths.
2) Add these two square together if you are calculating the longest side of the right angled triangle. Otherwise, take away the two squares.
3) Square root the answer from step 2.
Alternatively, you can use the formula a² + b² = c². Just remember that c is the longest side of the right angled triangle when you substitute your numbers into the formula.
Example
Calculate the value of x in this right angled triangle to 1 decimal place.

1) 7² = 49 and 2²= 4.
2) Since the longest side of the right angled triangle is being found then add these squares together.
49 + 4 = 53
3) √53 = 7.3 rounded to 1 decimal place.
5) Rounding off
As you seen in some of the questions already, you need to be able to round your answers off to the correct degree of accuracy.
The two systems of rounding that you will be tested on will be decimal places and significant figures. Decimal places are counted from the decimal point, whereas significant figures are rounded from the start of the number.
Example
a) Round 4864.3714 to 2 decimal places.
Here you are asked for 2 numbers after the decimal point, so the number will be rounded down to 4864.37 (since the number after the 7 is 1 which is less than 5)
b) Round 4864.3714 to 2 significant figures.
Here you are asked to round your number 2 places from the start of the number. Therefore the number will be rounded up to 4900 as the number after the 8 is 6 which is 5 or above.
As you can see the two systems of rounding give 2 different answers.
For some more maths help on rounding numbers off accurately click here:
How to round a number off to 1 significant figure (1sf or 1 sig fig)