What is a Truth Table in Symbolic Logic?
A
| B
| A ^ B
|
|---|---|---|
T
| T
| T
|
T
| F
| F
|
F
| T
| F
|
F
| F
| F
|
Basic Example
Frequently in symbolic logic, we make use of truth tables to help us determine the properties of an argument such as validity, consistency, and truth-functionality. These tables let us figure out how compound sentences operate when we give their atomic, or most basic, sentences truth values. It is a more visually-based method for seeing how logic is applied to our statements (Bergmann 75). So how do we make truth tables and then use them to help us reach these conclusions?
We first need a list of all the atomic sentences that we are using in the argument and assign all the possible truth value combinations which can be done to them (76). If I have the argument A ^ B, otherwise known as "A and B," both must be true if the argument is to be true. We put all the atomic sentences on the left and the argument on the right side of the table. Below them, each row will have the truth value assignments for each atomic sentence, then each one gets plugged into the argument and you work in steps, like in math, to determine if the argument is true or false. Making the table above shows that I have listed all the possible combinations for the pair of sentences we had. We filled out the final column based on the truth of the atomic sentences within. With the 2 atomic sentences A and B, we had 4 possible pairings.
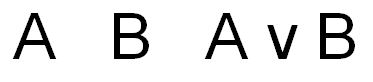
Formulaic Approach
Every time we add a new atomic sentence, we will double the number of possible combinations. 2 sentences give us 4 combinations, 8 give us 16, and so on and so forth. Mathematically speaking, if I have n number of atomic sentences, we will have 2n possible combinations for that group of atomic sentences. We will have 2n-1 T’s followed by 2n-1 F’s in the first column, then 2n-2 T’s, 2n-2 F’s, 2n-2 T’s, and 2n-2 F’s in the second column, until I am at the nth column, and have 2n-n = 20 = 1 T, 1 F, and so on (78).
Once you have created all the possible truth value combinations, you turn to your argument. Start by plugging in the truth value each time you see the atomic sentence in the compound. Then you will apply negations, if any exist, and place the new truth value underneath it. Finally, we look at each compound and determine what the overall truth value is based off the atomic sentences. Once we have the truth of that compound, we place that value underneath the connective of the sentences. Once we have the final truth value of the argument, we either place an arrow over that column or we circle it (79, 80).
For example, the argument A v (B ^ ~ C) is shown below. 3 atomic sentences are visible, so we expect 23 = 8 possible combinations, with 23-1 = 22 = 4 T’s in first column, then 4 F’s, 23-2 = 21 = 2 T’s, 2 F’s, 2 T’s, and 2 F’s in second column, and finally 23-3 = 20 = 1 T, 1 F, and so on. Plugging those values into each argument, we arrive at the conclusion of the argument which is presented in the center.
A
| B
| C
| A v (B ^ ~C)
|
|---|---|---|---|
T
| T
| T
| T
|
T
| T
| F
| T
|
T
| F
| T
| T
|
T
| F
| F
| T
|
F
| T
| T
| F
|
F
| T
| F
| T
|
F
| F
| T
| F
|
F
| F
| F
| F
|
Works Cited
Bergmann, Merrie, James Moor, and Jack Nelson. The Logic Book. New York: McGraw-Hill Higher Education, 2003. Print. 75, 78-80.
© 2013 Leonard Kelley








