How to Calculate the Volume of an Object
What is Volume?
The volume is the quantity of a three-demensional space. Think of it as the area of a three demensional space. Because the area is the quantity of a two-demensional space, we put a 2 in the top right corner. As such, when you find the volume of a space, you put a 3 in the top right corner. Let's say for example you were wanting to write 4 feet cubed. When you right it out, it should look like 4 ft³. When you are finding the volume of a figure, you can think of the number of cubic units that fit within its boundaries.
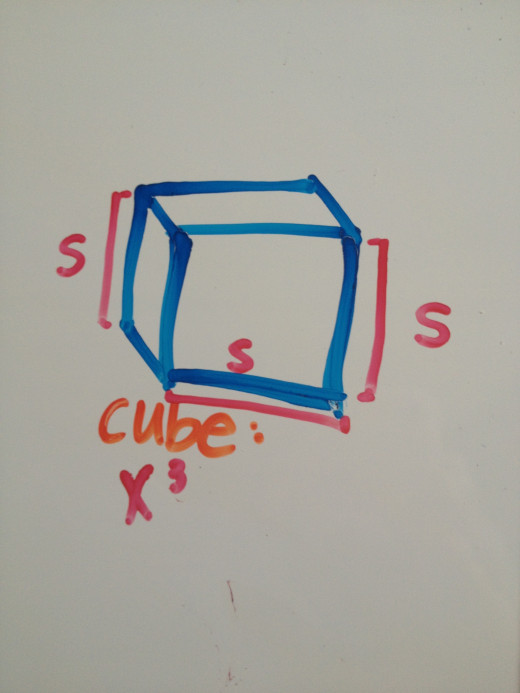
Find the Volume of a Cube
A cube is a three-demensional object with six faces on it. A cube is a three-demensional square. Because the shape is three-demensional, to calculate the volume we must use the height, width, and depth (or length). Just like the basic volume formula, you would use width x length x height to calculate the volume. But, since a square has all equal sides, we can use the formula x³ where x is the side of the square.
Example:
You need to find the volume of a cube with the sides of 3 inches.
- The formula for the volume of a cube is x³ where x is the side.
- Plug in the formula. x³ becomes 3³.
- Solve. 3×3 is 9. 9×3 is 27.
- Label. The answer is 27 in³.
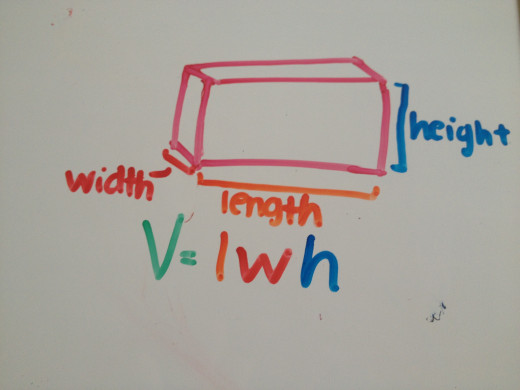
Find the Volume of a Rectangular Solid
A rectangular solid is a three-demensional shape with two rectangular faces that are identical connected to two other rectangles. Just like the cube, we need to calculate the volume with the length, the width, and depth (or length) of the rectangular solid. So, the formula to find the volume of a rectangular solid is volume = length x width x height.
Example:
You need to find the volume of a rectangular solid with a width of 4 cm, a length of 10 cm, and a height of 8 cm.
- The formula for the volume of a rectangular solid is length x width x height (or lwh).
- Plug in the formula. lwh becomes 4×10×8.
- Solve. 4×10 is 40. 40×8 is 320.
- Label. The answer is 320 cm³.
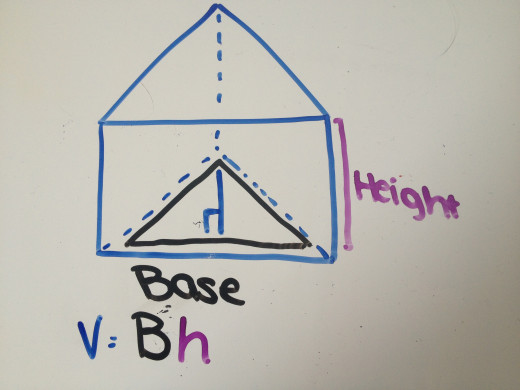
Find the Volume of a Prism
A prism is a solid figure whose ends or bases are the same size and shape and are parallel to one another. To find the volume of a prism, you must first find the area of the base. After you find the area of the base, you then multiply that by the height of the prism. So, the volume of a prism is Bh where B is the area of the base and h is the height.
Example:
Let's use the shape in the picture to the left. Let's say the triangle base's base is 8 cm and height is 6 cm. The height of the prism is 50 cm.
- The formula for the volume of a prism is Bh.
- Plug in the formula. Bh becomes (8×6÷2)50.
- Solve. 8×6 is 48. 48÷2 is 24. 24×50 is 1200.
- Label. The answer is 1200 cm³.
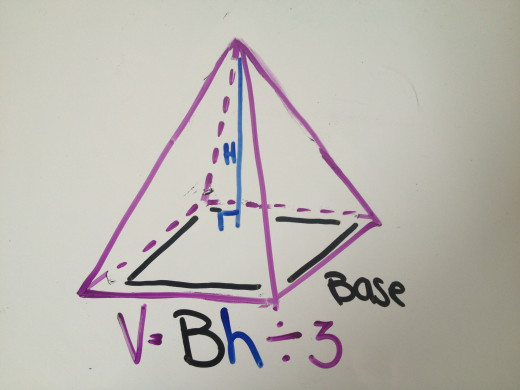
Find the Volume of a Pyramid
A pyramid is a shape that has a polygonal base and meets at a point called an apex. No matter what the polygonal shape the base is, the sides will always form a triangle. Finding the volume of a pyramid is similar to finding the area of a triangle. Also, finding the volume of a pyramid is similar to finding the volume of a prism in that you have to find the area of the base first. So, the formula for finding the volume of a pyramid is B x height ÷ 3. Where B is the area of the base.
Example:
Let's use the shape in the picture to the left. The sides of the base are 6 m. The height is 9 m.
- The formula for the volume of a pyramid is Bh÷3.
- Plug in the formula. Bh÷3 becomes (6×6)9÷3.
- Solve. 6×6 is 36. 36×9 is 324. 324/3 is 108.
- Label. The answer will be written as 108 m³.
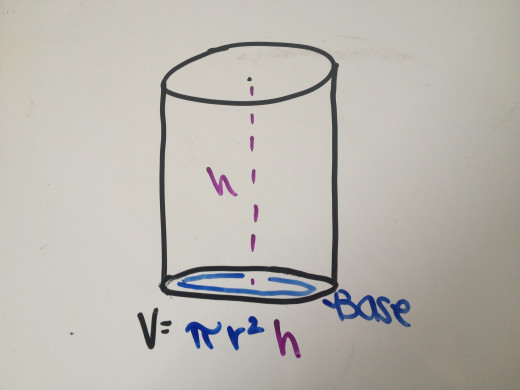
Find the Volume of a Cylinder
A cylinder is a solid that has two parallel bases connected by a curved figure. When you find the volume of a cylinder, you first take the radius of the base and multiply it by itself. If you are only given the diameter of the base, don't worry. The radius is half of the diameter. Divide the diameter by 2 and you'll have the radius. After you've multiplied the radius by itself, multiply it by pi (3.14...). Now, you should have the area of the base. After you've found the area, multiply it by the height of the cylinder. And voila! You have the volume of the cylinder.
Example:
You need to find the volume of a cylinder with a diameter of 10 yds and a height of 4 yds.
- The formula for the volume of a cylinder is πr²h.
- Plug in the formula. Oh wait! We don't have the radius. Since the radius is half the diameter, divide the diameter by 2. 10÷2 is 5 yds.
- Now plug in the formula. π5²4.
- Solve. 5² is 25. 25×π is 78.5. 78.5×4 is 314.
- Label. The answer will be 314 yd³.
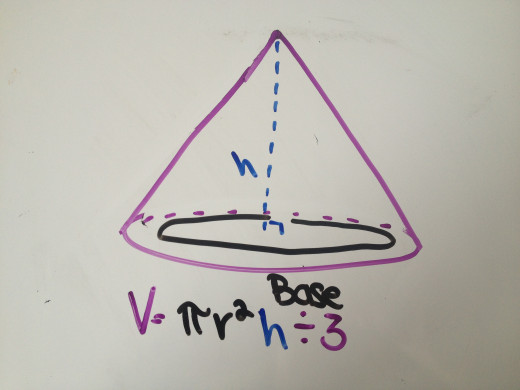
Find the Volume of a Cone
A cone is exactly like a pyramid except the base is always a circle. To find the volume of a cone, you need to find the area of the circle. To do that, you multiply the radius by itself (or square it) and multiply it by pi (3.14...). After you find the area of the circle (base) you multiply it by the height of the cone. Then, you divide the answer by 3. So, the formula to find the volume of a cone is πr²h÷3 where B is the area of the base.
Example:
Find the volume of a cone with a radius of 4 ft and a height of 6 ft.
- The formula for the volume of a cone is πr²h÷3.
- Plug in the formula. π4²6÷3.
- Solve. 4² is 16. 16×π is 50.24. 50.24×6 is 301.44. 301.44÷3 is 100.48.
- Label. The answer is 100.48 ft³.