How to Make Measurements the Scientific Way
Introduction
Of course you probably know how to make a simple measurement with a ruler. Scientists make gathering quantitative data more difficult than most people are used to. However, it is for a good cause: by making measurements to the correct number of significant digits, they communicate the precision of the measuring equipment with which they obtained the measurement. In order to make the process simpler, each variable will be expressed with a letter as a symbol.
n is the numbered mark which the measured object has met or exceeded.
u is the number of unmarked lines which the measured object has met or exceeded, past n.
v is the value of each mark. To find the value, take any numbered mark and subtract from it the numbered mark that immediately precedes it. Then divide that number by the amount of spaces between them.
Δ is the uncertainty. To find the uncertainty, divide v by 10.
i is imaginary marks in which the measured object has met or exceeded. Essentially, what is being done is inventing 10 new marks (from the uncertainty value) and imaging how many the object touches.
Example Measurement
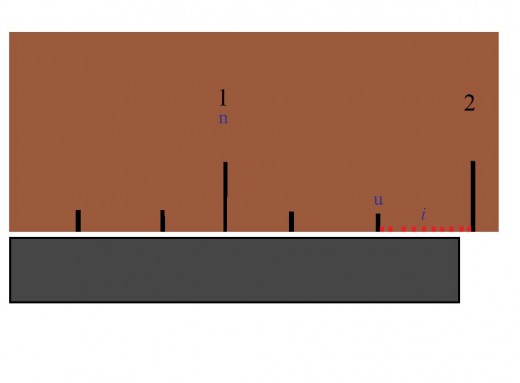
Example
In this example: n=1, u=2, v=.3, Δ=.03, and I have imagined i as 9. someone else could have claimed that i=8. Since this value is uncertain, and the red marks do not really exist on the ruler, it is subjective to each observer. The equation is 1+(2·.3)+(.03·9) which comes out to 1.87. Then one would assign the units. Since I had not previously specified, I will now designate it as inches. The measurement of the bar is 1.87 inches.
A Small Bit of Science and Math
A scientific measurement is an equation that is resultant from these variables. The equation is: n+(u·v)+(Δ·i ). At this point, it is important to discuss certainty. The values n, u, v and Δ are certain. This means that they should be agreed upon by all observers. i is an uncertain value, which means it may differ from observer to observer. Notice that the value of uncertainty is certain (because, in this case, the uncertainty is derived from an elementary mathematical operation from a certain value). However, in the actual equation, one is multiplying a certain value by an uncertain value (Δ·i ), and so the result will be uncertain. This is important, because the significant digits are all of the certain digits, plus one uncertain digit. Since all of the certain digits will always agree, the only value that should change is the one uncertain digit (which is the last digit on the right). In addition, each piece of equipment with the same value for marks and the same number of spaces between them (in other words, same precision) will yield the same number of significant digits.
More Important Equations for Measurements
There are a lot of other important mathematical operations for making scientific measurements. Typically a scientist will make at least three measurements under the same conditions. They will then average the measurements. ̅x =Σx/nt where ̅x is the average, Σx is the sum of the trials (x1+x2+x3...xn), and nt is the number of trials. Root mean square is expressed as: ((1/n)[x12+x22+x32...xn2])1/2 . Then, the deviation is found by d=|(x- ̅x)|. Of course, the average of the deviation must be found. ̅d=Σd/nt. The relative error is a consideration of the random error inherent within the measuring equipment and is found by: %RE=(Δ/cv)(100%) where cv is the "correct value" of the measurement. The relative average deviation is derivative of the precision (how closely grouped the values are) of the measurements. %RAD=( ̅d/ ̅x)(100%). Finally, the error is indicative of the accuracy (proximity to the correct or accepted value). The percent error is given by: %Err=|([ ̅x-cv]/cv)|(100%).
Sources of Error
Another aspect of measurements is determining the sources of error. This, combined with modifying an experiment to mitigate sources of error, is a study all on its own. There are infinite sources of error, with different magnitudes of influence and different difficulty in corrective actions. Examples include, but are certainly not limited to: parallax error; temperature/pressure difference from start to finish of lab (volumetric thermal expansion); adhesion of liquid to glassware during transfer; residual liquid in glassware during transfer; re-absorption of environmental water vapor; atmospheric contaminants (dust particles, etc.); heavier/lighter isotopes; vibrational contamination (sound, compression waves from earth moving or thunder, etc.); imperfect shapes (if calculating volume from dimensions), impure chemicals; improperly calibrated equipment; misjudgment on thorough completion of reaction (particularly with equilibrium reactions); reaction time error (both equipment and observer).
Possible Modifications
There are methods of modifying experiments to lessen the probability or impact of the aforementioned errors to occur. Examples include: making all measurements from the same position, which should be at eye level; performing the laboratory in a stable environment that is free of contaminants (temperature/pressure controlled, air filtered, vibration absorption, possibly even in a vacuum chamber); use verified pure reagents (free of contaminants and verified atomic mass); perform complete measurements to verify geometry; eliminate residue from glassware; use glassware that prevents adhesion.