How to Reduce Fractions
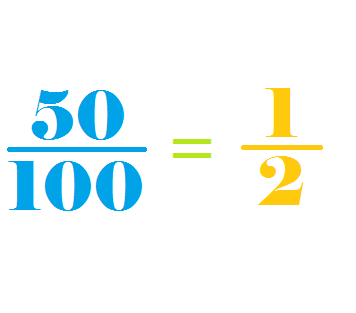
Why do we simplify or reduce fractions? We reduce fractions because it makes math and life simpler! If I said I have 8/16 of a pizza you probably would have to stop and think about how much that really is. 8/16 is the same as 1/2. If I said 1/2, you'd probably know right off the bat how much that is. Reducing fractions is easy. If you want to know more about reducing fractions, read on!
What does 'divisible' mean?
(of a number) capable of being divided by another number without a remainder.
For example: 24 is divisible by 4 because 4 times 6 is 24
Reducing Fractions to Lowest Terms
What is reducing fractions to their lowest terms? Essentially, we are making the fraction as small as possible. To reduce a fraction to its lowest terms is very easy. All you need to know is division. To reduce the fraction to lowest terms, you need to find out if a certain number is divisible with the numerator (the top number) AND the denominator (the bottom number). A number is divisible by another if, when you divide them, you don't have a remainder.
Tips and Tricks for Divisibility
You don't always have to do division in order to find out if a number is divisible with another.
- A number will be divisible by 2 if its last digit is an even number.
- A number will be divisible by 3 if the sum of its digits is divisible by 3.
- A number will be divisible by 4 if the number formed in the last two digits is divisible by 4.
- A number will be divisible by 5 if the last digit is a 5 or a 0.
- A number will be divisible by 6 if it's also divisible by 2 and 3.
- A number will be divisible by 9 if the sum of its digits is divisible by 9.
- A number will be divisible by 10 if the last digit ends in a 0.

The first step...
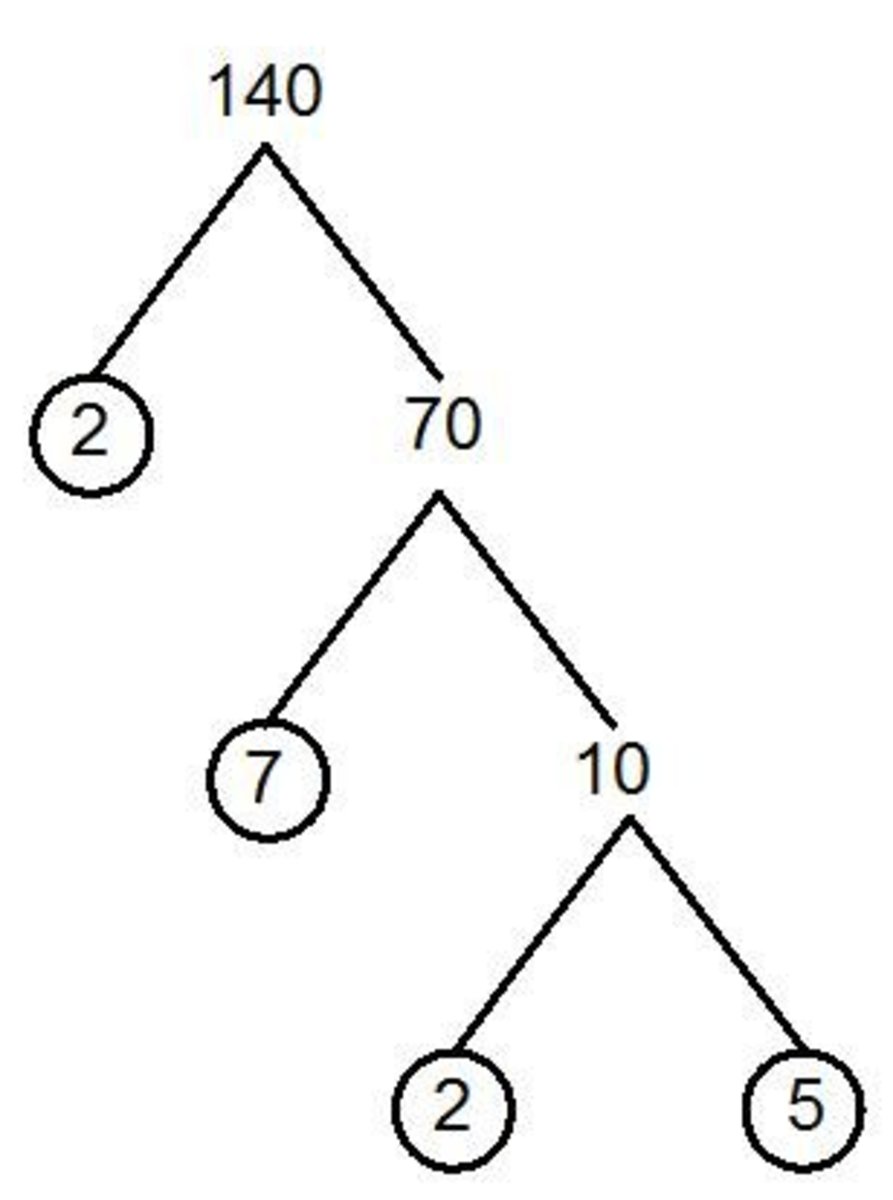
To reduce a fraction to lowest terms, you must first take the original fraction and find all the factors of the numbers. For an example, we'll use the fraction 48/120.
Let's start with 48 and find all the factors. We know that 1 and 48 are factors because 1*48 is 48. 2*24 is 48...so on a so forth. Follow the divisibility tips and divide. Remember, a number doesn't go into 48 evenly, it's not divisible thus, not a factor. By the time you are done, you will discover that the factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.
Now let's do 120. Follow the same steps with 48 except plug in numbers for 120. 1*120 is 120 so 1 and 120 are both factors of 120. 2*60 is 120 so 2 and 60 are also factors of 120. By the time you are done with this number, you will discover that 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, and 120 are all factors of 120.

After you find the factors...
After you find the factors, look for all the matching factors between the numerator and denominator. By doing this, you are finding all the common factors.
The common factors between 48 and 120 are 1, 2, 3, 4, 6, 8, 12, and 24.
Now you want to find the greatest common factor (or the GCF for short.) The greatest common factor of 48 and 120 is 24 because it is the highest common factor between the two.
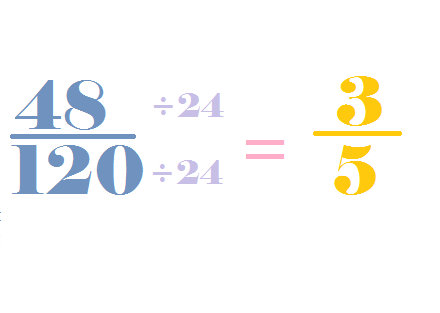
Now comes the fun part...
After you find the greatest common factor, you can finally simplify the fraction. To do this, you must divide the numerator and the denominator by its GCF. In this case, the GCF is 24.
Let's start with the numerator. 48 divided by 24 is 3. The new numerator is now 3.
Do the same to the denominator. 120 divided by 24 is 5. The new denominator is now 5.
Double check that you cannot reduce the fraction anymore. The only numbers that go into 3 and 5 are 1 and itself. Therefore, it cannot be reduced anymore.
Your reduced fraction is now 3/5. Congratulations! You just reduced a fraction!