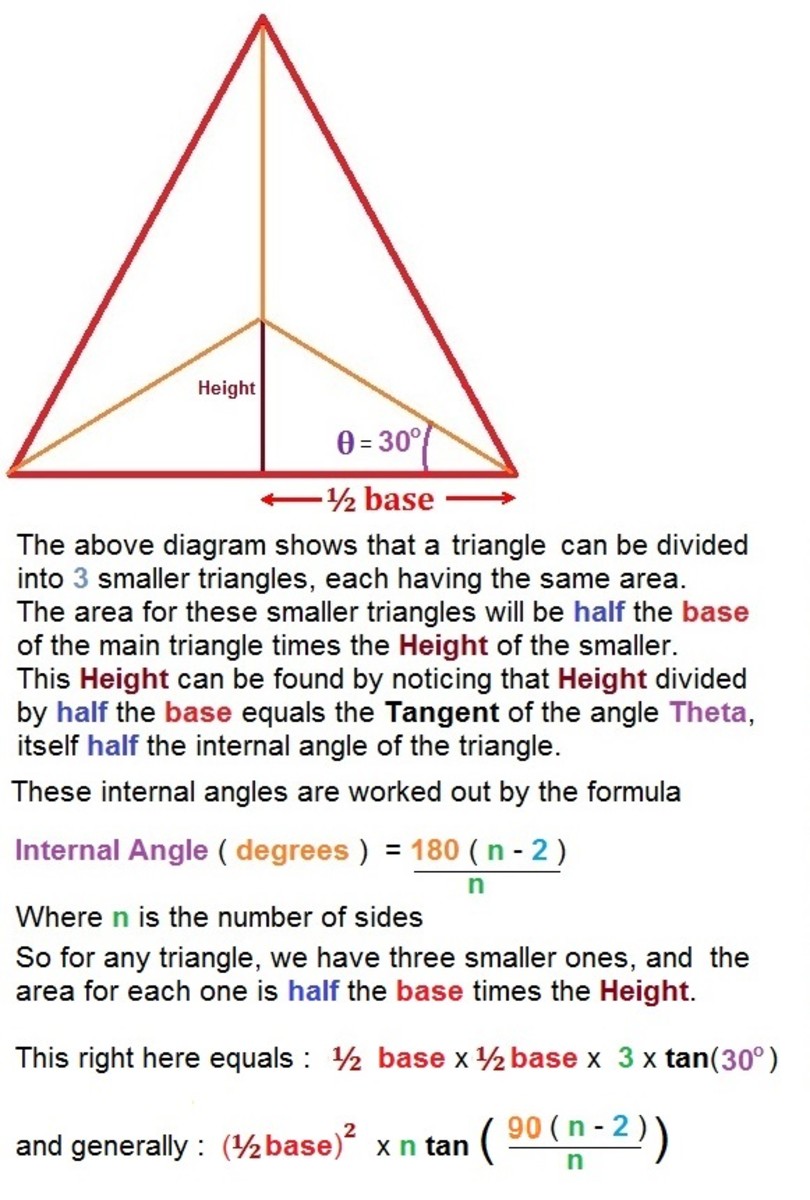
How to calculate the amount of sides of a regular polygon from the interior or exterior angle.
In this hub you will shown how to work out the number of sides of a regular polygon if you are only told the interior angle (the interior angle is the inside angle). First subtract the interior angle from 180⁰ - this will give you the exterior angle of the regular polygon since the interior and exterior angle both add up to 180⁰. All you need to do now is divide this number into 360⁰.You can sum this up as a formula:
Number of sides = 360 ÷ (180 – Interior angle)
Example 1
The diagram shows part of a regular polygon. Calculate the total amount of sides of the regular polygon.
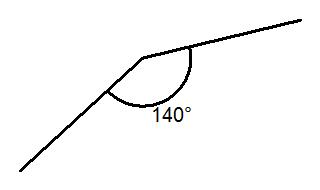
From the diagram you know the interior angle which is 140⁰.
Firstly, subtract this number off 180⁰ to give the exterior angle of the regular polygon:
180 – 140 = 40⁰.
Finally, divide 360⁰ by the exterior angle to give the total amount of sides of the regular polygon.
360 ÷ 40 = 9.
So the regular polygon is a nonagon as the polygon has 9 sides.
Alternatively, you could have substituted the interior angle into the formula above:
Number of sides = 360 ÷ (180 – Interior angle)
= 360 ÷ (180 – 140)
= 360 ÷ 40
= 9 sides
Example 2
The diagram shows part of a regular polygon. Calculate the total amount of sides of the regular polygon.
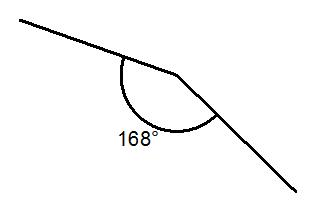
From the diagram you know the interior angle which is 168⁰.
Like example 1 first subtract the interior angle off 180⁰ to give the exterior angle of the regular polygon:
180 – 168 = 12⁰.
Finally, divide 360⁰ by the exterior angle to give the total amount of sides of the regular polygon:
360 ÷ 12 = 30.
So the regular polygon has 30 sides in total.
Alternatively, you could have substituted the interior angle into the formula above:
Number of sides = 360 ÷ (180 – Interior angle)
= 360 ÷ (180 – 168)
= 360 ÷ 12
= 30 sides
Sometimes, you might be given the exterior angle instead of the interior angle of the regular polygon. If this is this case don’t both with the first step and just divide 360 by the exterior angle.