How to find the Sum of the Angles For Any Polygon

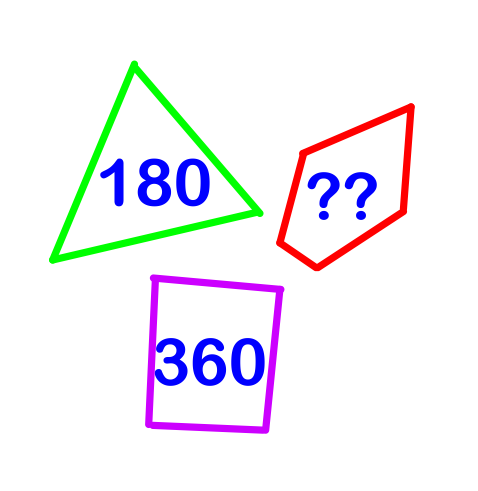
We know that a triangles angles add up to 180 degrees. We also know that a quadrilateral, such as a square has angle measures that add to 360 degrees.

So how to we find the sum of the angle measures for a pentagon, hexagon, or a shape with any number of sides?

First we need the formula in order to calculate the sum of the angles. We need to know how many sides the given figure has in order to find this.

To find the sum of the interior angles for any polygon we use the formula below

180(n-2)

with n being the number of sides that the polygon has

So for example let's start with the triangle, n = 3 because a triangle has 3 sides

180(3-2) = 180 * 1 = 180

Quadrilateral, n=4

180 (4-2) = 180 * 2 = 360

Pentagon

A pentagon has 5 sides

n=5

180(5-2) = 180 * 3 = 540

Hexagon

A hexagon has 6 sides

180(6-2) - 180 * 4 = 720

Essentially every time you add a side to a figure you add another 180 degrees to the sum of the interior angles. Two angles do not create any interior angles so therefore they can not add to 180. The first angle that can create a shape that has interior angles has 3 sides so therefore subtracting the original two sides from the equations allows you to find the correct sum of interior angles.