How to add fractions together
Adding fractions may seem complicated at first, but it's really not that hard.
Here are three words that we should define at the beginning:
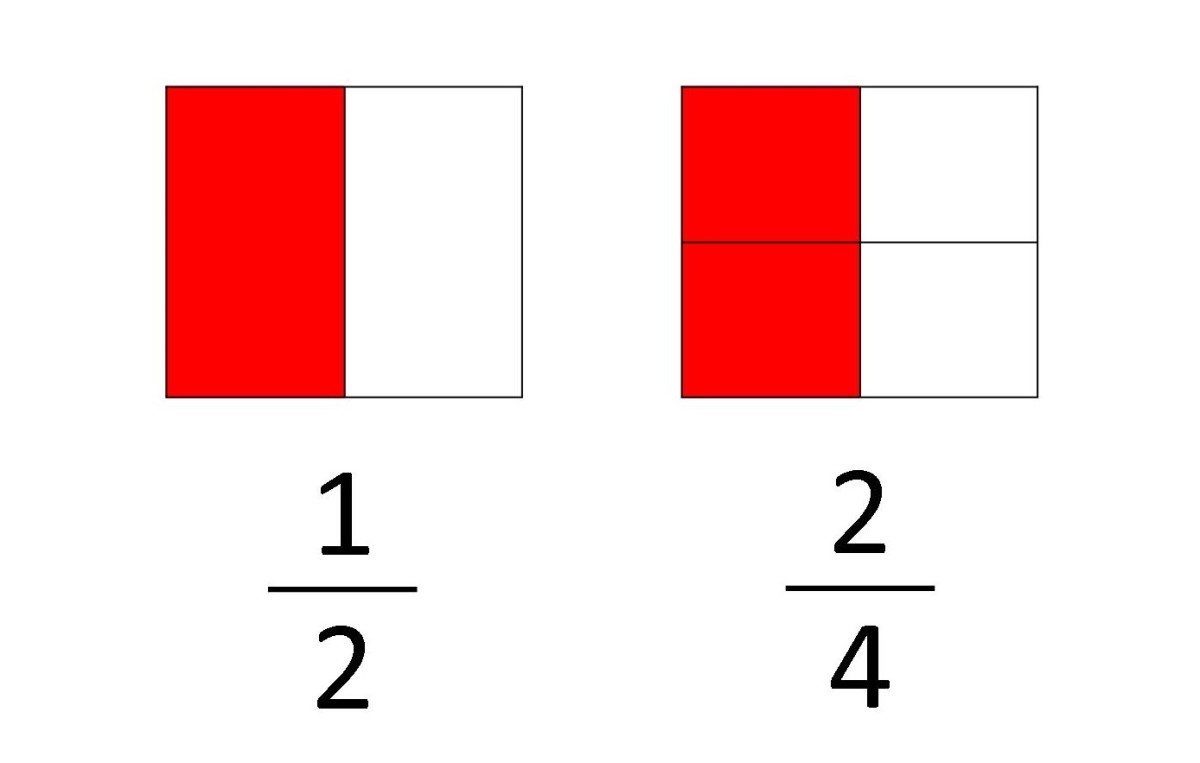
1) Numerator - the top part of the fraction
2) Denominator - the bottom part of the fraction
For example, for the fraction 2/3:
- 2 is the numerator
- 3 is the denominator.
3) LCD - lowest common denominator - the smallest number that all the different fractions' deminators will go into without giving you a remainder.
For example, for the fractions:
1/3 + 1/4 + 1/5
There are 3 denominators: 3, 4, and 5. The LCD for these is 60. 3, 4 and 5 all go into 60 without creating a remainder.
There are other common denominators for 3, 4 and 5, including 120 and 240, but these are larger than 60, so they are not the LCD.
Hint: A quick way to find the LCD is to multiply the denominators together. However, sometimes this just creates a larger common denominator than the LCD, in which case you'll have to reduce the final fraction in your answer.
When the denominators are all the same
When all the denominators are the same, it's easy: Add up all the numerators, and put them over the same denominator.
For example:
1/12 + 3/12 + 5/12
= (1+3+5)/12
= 9/12, which you can reduce to 3/4
Another example:
2/17 + 3/17 + 10/17
= (2+3+10)/17
= 15/17
Easy, right?
Have 8 minutes? You can learn how to add fractions by watching this video
When the denominators are different
Okay, here's where it gets a little trickier--but don't panic! Just follow this procedure. Let's start with an example:
1/3 + 2/9 + 3/10
1) Find the LCD for all the denominators.
For 3, 9 and 10, the LCD seems to be 90. All 3 numbers go evenly into 90 without a remainder.
2) For each of the denominators, find out how many times it goes into the LCD.
For 3: 3 goes into 90 30 times
For 9: 9 goes into 90 10 times
For 10: 10 goes into 90 9 times
3) For each of the original fractions, multiply the numbers you get in (2) to both the numerator and the denominator.
1/3 + 2/9 + 3/10 becomes
(1x30)/(3x30) + (2x10)/(9x10) + (3x9)/(10x9)
which, if you multiply out the numerators and denominators, becomes:
30/90 + 20/90 + 27/90
WAIT! Now they all have the same denominator! You can apply the procedure in the gray box above now:
= (30+20+27)/90
= 77/90
There's your answer!