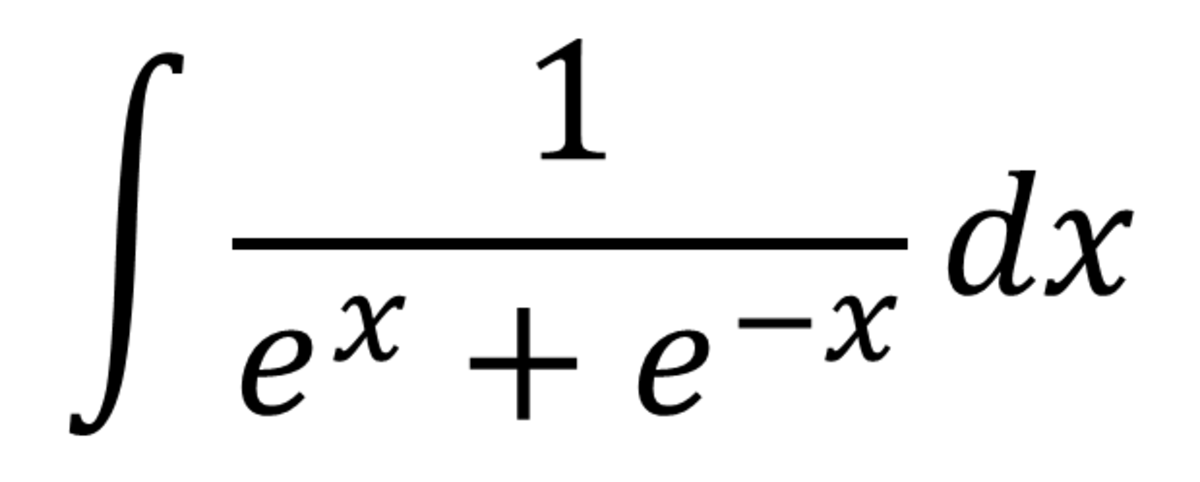Integration-Pt 1-Transforming an Inverse Trigonometric Expression into an Algebraic one.
THE CONDITION FOR UNCONDITIONAL:
1. All my math hubs have something about God in their final paragraph(s). Paragraph 12 of this hub addresses the condition for God's unconditional love.
INTEGRATION AND MATHEMATICAL MANIPULATIONS:
2. There are two main branches in calculus: differentiation, and integration. To do differentiation in a 1st year calculus course requires following the rules and doing the arithmetic. To do integration you have to be a sage, a prognosticator, a clairvoyant, and mostly a by-guess-by-golly type of person. You take a guess, and by golly it worked. Some of the techniques to do integration are absolutely brilliant. Integration by parts, logarithmic integration, Taylor expansion, converting to polar coordinates and trigonometric substitution are just a few of the many techniques developed, and which can be used to perform integration. Although I may be easily impressed, I think they are all very clever. They all boil down to being mathematical manipulations which can make evaluation of the integral easier.
WHAT IS TRIGONOMETRY IN A NUTSHELL?
3. Well, it depends on the size of the nutshell in order to easily explain it. Let's make it in the shape of a rectangle with 625 feet for its length, 104 feet for its width, and the roof will be an all glass cover in the form of an ark--oh excuse me-- arc. The length will run south to north, and if you are lying in a sleeping bag on your right side at the extreme southern end, you want to be able to open your eyes and see the north star. You happen to know that the angle you must turn your eyes from the floor is about 31 degrees( 31.2333 to be exact) in order to see the north star. So what height must you limit the walls enclosing this rectangular "nutshell" so that you can see the north star from the southern end? This is what trigonometry( trig) does. It relates the 2 sides( the floor and the wall), and also the hypotenuse( the diagonal line directly from your eyes to the tip of the northern wall) to one another. Having knowledge of how those relationships work together is what trig is all about, and it enables one to solve an enormous amount of problems in physics, engineering and many other fields. In this case the wall must be 625( tan 31°)=375.54 feet, or round down to 375 feet. I suppose I could have made this nutshell 120 times smaller and still made my point, and even at that size I would still have plenty of room to put all my important papers. Well, I have to plant a tree 34 miles east of here, but I only have 47 minutes to get there. Doesn't sound too tough but all I have is my horse, and even Secretariat could not run that fast.
INVERSE TRIGONOMETRIC FUNCTIONS:
4. Entire textbooks are written about trig, and several chapters are dedicated to the subject in precalculus textbooks; therefore, in this hub we will only take a peek at some of the pertinent concepts.
5. At L1 cot stands for cotangent, and cot--1 stands for inverse cotangent, or arc cotangent. cot--1 represents the angle for that value of cotangent, and it is another way to write the angle, θ. One way to think of it is "arc" is the arc made by that angle, θ( or cot--1). So the notation at L1 means the same thing as the notation at the first line of L7. The second line of L7 is a trigonometric identity( trig ID) that equals the first line.
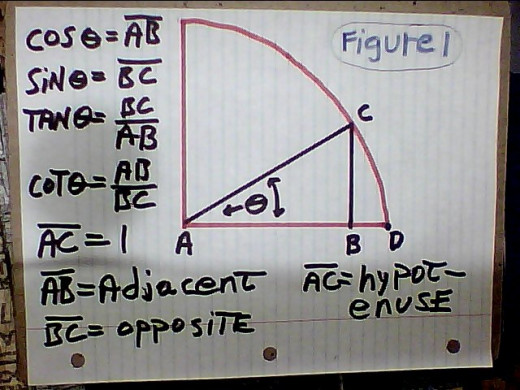
FIGURE 1 EXPLAINED:
6. Transforming an inverse trig function to an algebraic one is a very effective way get it in a form that you can integrate. Trig is fundamentally all about the right triangle. When you can get this in your head, then you are well on your way to do the manipulations necessary to do these conversions.
7. Figure 1 represents (1/4)th of the unit circle in the 1st quadrant. The unit circle has a radius of one; therefore, the length of line AC is 1 unit( foot, mile, inch, cm, meter, whatever). Both cosine( cos) and sine( sin) are defined as AB / AC, and BC / AC respectively, but since AC is 1 then they reduce to what is shown in figure1. The angle, θ, is, in this case, about 31 degrees. The terms at the bottom of fig.1 are those normally used in trig to describe the 3 sides of a right triangle. Arc CD is the arc on this unit circle that is made with angle θ.
L1 THROUGH L5 EXPLAINED:
8. The first thing to do to convert L1 to its algebraic equivalent is to define the angles at L2 and L3. You may have read that a function is like a machine that operates on something. You put a value into it, and it cranks out another value( sometimes the same one). This is what the cotangent( cot) function does. You put a value for the angle, θ, and it cranks out a value for line AB divided by BC. Trig has been developed to the point that we know what the lengths of AB, and BC will be at a specific angle. At L2 if we take the cotangent of the left equation then we will get the right equation. Taking cot( cot--1u) cancels out leaving just u. It is similar to multiplying 13 by 1/13 and you are left with 1. Now we know that u is the value of cot θ1. That is telling us that AB / BC is u. The only way it can be u is if line BC has length 1, because any number divided by 1 is that number. So we put that length on L4, and we put the length of u onto the adjacent leg at L4. We then calculate the length of line AC using the Pythagorean theorem, and place that at L4. We do all of that for θ2 at L3. I have a subscript of 1 there at the left side but it is supposed to be 2. The math here is forcing us to leave the unit circle, right? We already have length of 1 for BC; therefore, in this case the length of AC must be greater than one.

L6 THROUGH L8 EXPLAINED:
9. L6 is just a reminder of how cotangent is defined. As I said at paragraph 5, L1 and L7 say the same thing; therefore, we write it in standard form at L7, and then give the trigonometric identity at the 2nd line of L7, which represents the 1st line of L7. The rest is really easy. We know the representations of sine and cosine given at figure 1; therefore, we plug these values of them at L4, and correlate them with the 2nd line of L7, and place them on the 3rd line of L7. L8 is just doing the arithmetic to simplify L7, and our final answer is at L8. This is the algebraic representation of L1, and it is in a form that we can integrate.
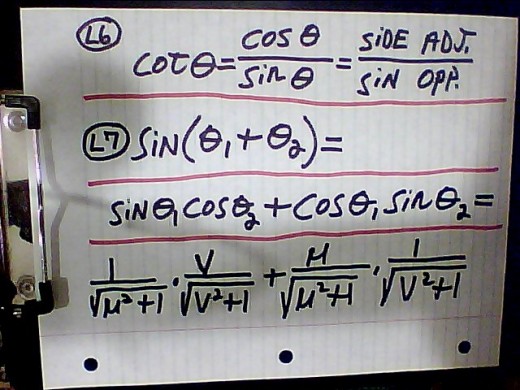
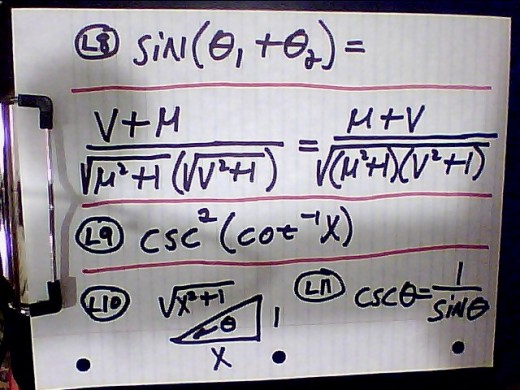
L9 THROUGH L15 EXPLAINED:
10. At L9 csc stands for cosecant, which is the reciprocal of sine; therefore, it is( from fig 1) AC / BC. So L9 says to square the value of csc θ. We already know how to represent arccotangent X. Here cot -1(X) is just being used to represent the angle, θ. The triangle at L10 was explained at paragraph 8. Sine θ is defined at L12. Since cosecant is the reciprocal of sine then the 2nd line of L12 represents that. After squaring that value we have the final answer at L15, and this is very easy to integrate. Integrating we have ∫ X2 + 1 dx gives and answer of (1/3)X3 + X + C( a constant). L9 would have been much more difficult to integrate if we had not converted it to its algebraic representation.

MUCH EASIER INTEGRATION IS ACHIEVED:
E1. These are edits I finished on 11-19-2012: You can try and integrate L9 without first transforming it into its algebraic equivalent, but it would be much more difficult. At EL1 I write L9 in a form that my Ti-89 will recognize. At EL2 I tell the ti-89 to integrate it, and I get EL3. The integral sign applies to the entire fraction, not just the denominator. Notice my ti-89 did not integrate it at EL3. If I put in limits of integration as at EL4, then the ti-89 can give me the answer of 2.0253 at EL4.
E2. Look how much easier the integration is at EL5 through EL7. The integrand at EL5 is the algebraic equivalent of L9, and it is so easy to integrate, one can do it without a calculator. We get the same answer at EL7.
E3. EL8 is showing that EL2 and EL3 are the same function with the angle in the first quadrant. The ti-89 gives, of course, the same answer.
E4. You must be aware of the domain when doing these transformations. I kept the angle in the first quadrant to keep it simple.


WHAT IS NEXT IN THIS SERIES?
11. The final answer at L8 will be integrated in part 2 of this series on integration. We will look at the difference of θ1 and θ2 being two different angles on a plane, or two different angles in three dimensional space. In future hubs I'll address some of the techniques of integration mentioned at paragraph 2.
WHEN IS GOD'S LOVE UNCONDITIONAL?
12. This is a continuation of paragraphs 12, 13, 14, 15, and 16 of hub#12.9. I believe God's love is unconditional concerning who can repent and then be saved. Scripture is very clear on this. God is not willing that ANY perish, but that ALL should come to repentance( 2 Peter 3:9). It does not matter who you are or what you did: all means all. God would not command ALL people to repent( Acts 17:30) if He did not expect that all people had the ability to repent; nor would God send the "all likewise perish"( Luke 13:3 and 5) people to eternal hell if they did not ALL have the ability and choice to live eternally in heaven with Christ if they repented. The offer to choose Christ is to all people( Joshua 24:15; Deuteronomy 30:15 to 19; 1Kings 18:21). Whosoever means whosoever; therefore, John made it very clear that ALL people have the ability to choose live, or death; to choose Christ, or sin; to choose heaven, or hell( John 3:16; 4:14; 11:26; 12:46; 1John 3:6 and 9; 4:15; 5:1 and 18; 2John 1:9). So in this respect God's love is unconditional---ANYONE CAN CHOOSE LIFE! There are no conditions given with these verses. None of them say all or whosoever, except those of you who did this or that, or did not do this or that. People come to Christ at different times in their lives, and you can be sure that many of them have had a questionable( to put it mildly) past. Regardless of how sinful one's life has been, God's love is unconditional--according to the Scriptures given--concerning God's offer for that person to choose life( i.e. obey Christ; obey God's Word), and be saved from eternal hell, and to eternal joy and rest in God's kingdom.