Inverse proportion word problems with graphs ( the meaning of y is inversely proportional to x)
If y is inversely proportional to x then the formula connecting y and x is y = k/x (k divided by x). k is known as the constant of proportionality which can be found by using the boundary conditions. The boundary conditions are the values of x and y which are given in the question.
Example 1
If m is inversely proportional to n, and when n = 7 m = 8, find a formula for m.
Since m is inversely proportional to n then the formula is:
m = k/n.
All you need to do now is use the boundary conditions (n=7 and m=8) to calculate the value of the constant of proportionality. You find k, by subbing in these values into your formula:
8 = k/7.
Since k is being divided by 7, then all you need to do is multiply the 8 by 7:
8 × 7 = k
56 = k
You can now put this value of k back into the original formula:
m = 56/n
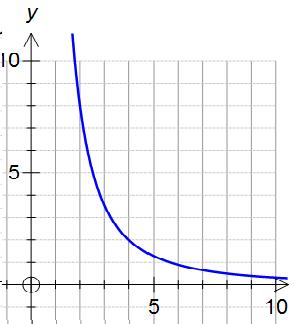
The graph of m and n is shown below. Notice that as n increases, m decreases. This is an example of inverse proportion.

Example 2
If p is inversely proportional to q², and when q = 4 p =2, find a formula for p.
Since p is inversely proportional to q² then the formula is:
p = k/q².
All you need to do now is use the boundary conditions (p=2 and q=4) to calculate the value of the constant of proportionality. So like example 1 sub these values into your formula:
2 = k/4².
You can now work out 4²:
2 = k/16
Since k is being divided by 16, then all you need to do is multiply the 2 by 16:
2 × 16 = k
32 = k
You can now put this value of k back into the original formula:
p = 32/q²
The graph of p and q is shown below. Notice again that as q increases, p decreases.
Now you have mastered inverse proportion, check out this next hub on direct proportion:
Direct proportion. How to write down a formula if y is directly proportional to x. Maths GCSE.