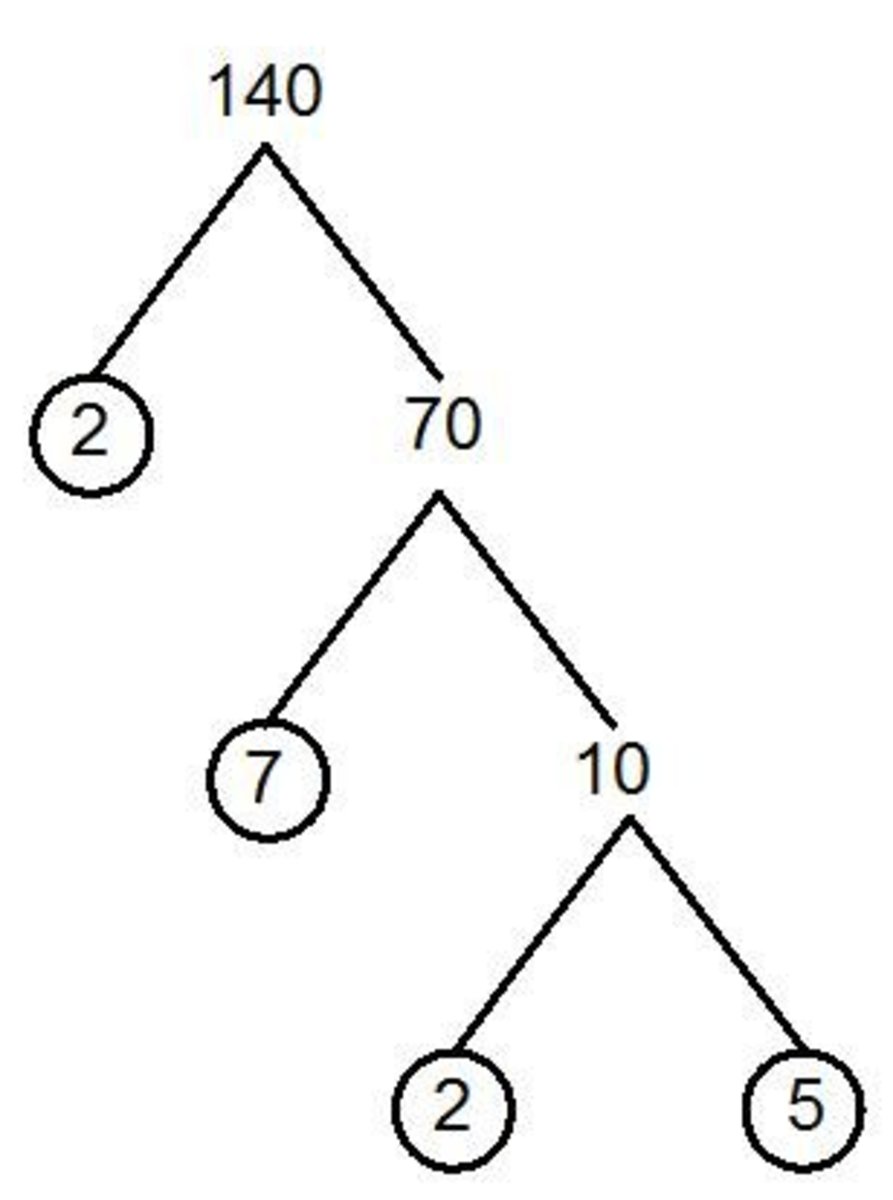
It's prime time for prime numbers.

Prime numbers are something we learn around 4th or 5th grade. Many of us take this for granted.

Until...............................

They ask us a prime number question on the SAT test. Why did they do that?

If we don't know prime numbers, we can't factor fractions. Their usefulness carry all the way the way through calculus. Prime numbers give us the idea of divisibility of higher order numbers. Whether it is factoring or doing trigonometry or vector calculus, the idea of prime numbers helps us understand complex components of numbers and how they can be made basic. After all prime numbers are numbers that cannot be broken apart. You will be amazed at what you can do when you fully realize prime numbers.

Reducing fractions will be a snap. You will understand better how to factor polynomials. Many logical problems will be easier to see with your newly gained knowledge. Prime numbers are a base concept and unfortunately they are not well taught in schools. They are often thought as a peripheral concept that is not real important. In this hub, I will lay a foundation for prime numbers including the numbers that are prime up to 100 and how to determine if a number is prime or not. This will be a continued series.

But first the definition:

A prime number is a integer that can only be divided by itself and one.

So 13 is prime because 13 can only be divided by 1 and itself.

14 can be broken down into 2 x7 therefore it is not prime number.

Hey this isn't too bad is it?

We are going to start with a few rules:

1) 1 is not a prime number and this is by definition.

2) 2 is the only even prime number.

3) Prime numbers cannot be negative integers.

Hey not too many rules. I like this already. Okay here are the first primes under 100.

2 3 5 7 11 13 17 19 23 29

31 41 43 47 53 59 61 67 71

73 79 83 89 97

So how do we know if the number is prime? I am amazed at how often people do not understand this. It seems as though it is just magically this way............Hey it looks like nothing can go into this number. Well there is a rationale to finding prime numbers.

First some quickies to make our job easier. No even integer except 2 is prime. Pheew, that is half the numbers out of the way. No number that ends in 5 , except of course 5 is prime (15 is 5 x3, 25 is 5 x 5, and 625 is 5 x 125).

So how do we see if 89 is prime? We start by dividing by all the primes except 2 and 5 and keep going successively larger when the number does not evenly divide into the number we're testing.

Lets begin.
We first see if the number is divisible by 3
then by 7,
and then by 11.

Hey, none of these numbers divide into 89. It is prime.

Why did I stop at 11? Well, I am glad you asked. If the numbers square is larger than the number itself we have tested all possible. Hey, if there is one number higher than the square then there has to be one lower. We already tested the lower numbers.

Hey lets try 191 (which by the way is prime).

We start with 3 and it isn't divisible, then 7, 11, 13, 17. All not divisible and 17 squared is 289. 191 is therefore prime.

How about 341? Okay not divisible by 3, and not 7. Whoa it is divisible by 11 (11 x 31)!

Yes that is it. If you want to find out if a number is prime, just divide by the prime numbers until you reach a number whose square is larger than the number you are testing. Voila, you have found a prime number.

In a later hub coming here real soon ,we will learn about prime factorization (GCF, LCM, combining fractions) the first 1000 primes ending in 1, 3 , 7, and 9. Lots of good stuff.