Kepler's Equation
Imagine a planet moving around a central star of the mass m. Let we know two essential parameters of its ellipse, the major semi-axes a and the eccentricity e. What is a position of the planet in time t since the last periapsis? In this article we will show how to answer this question, using Keplers's Equation.
Questions like this are related to the problems known as “one body problem” and “two body problem” in classical mechanics. More precisely, the branch of astronomy that deals with motions of celestial bodies is called celestial mechanics. With knowledge in this field we are able to forecast coming eclipse, occultations, possible crashes of celestial object etc.
Position parameters
A position of the body moving along an ellipse (more generally, Keplerian orbit can be ellipse, parabola or hyperbola) is usually described with two parameters:
- orbital position vector r and
- true anomaly f,
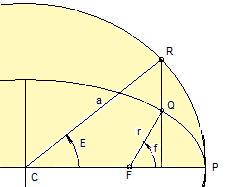
as it is depicted in Figure 1. Thus, answer on the question above should be length of the vector r and the value of angle f.
There are three angular parameters that define a position along an orbit. In addition to true anomaly f, there are the eccentric anomaly E and the mean anomaly M. True anomaly is the angle between the direction of periapsis (FP) and the line connecting focus and the body (FQ). The eccentric anomaly is the angle between major semi-axis and the direction from the center of ellipse to projection R, as seen from the center of ellipse. The point R lays on the circle with radius a which center correspond with the center of orbit; where direction RQ is orthogonal to CP.
The main anomaly is the only parameters among the three which is not an angle. Instead, this parameters shows proportion of the area "swept" by the FQ line since the last periapsis. Thus, the value of M increases from 0 to 2π radians during one cycle. It holds relation (1), where t-t0 is the time elapsed since moving from P to Q and T is orbital period. Orbital period is the duration of one full orbit. (All relations mentioned in this article are presented in Figure 2.)
Parameters the main anomaly M, the eccentric anomaly E and the eccentricity e are connected by the relation (2) that is called the Kepler's Equation.
Calculating M for a known E is straightforward, whereas calculating E for a given value of M is much more complicated and cannot be solved algebraically (we will show numerical solution in the next paragraph).
The following is the algorithm solving the Kepler equation (2). Once when eccentric anomaly is determined the values of r and f follow straightforward from the relation (5) and (6).
Eccentricity
| Curve
|
|---|---|
e>1
| hyperbola
|
e=1
| parabola
|
e<1
| ellipse
|
Table 1. Any conic section can be the path of a celestial body.
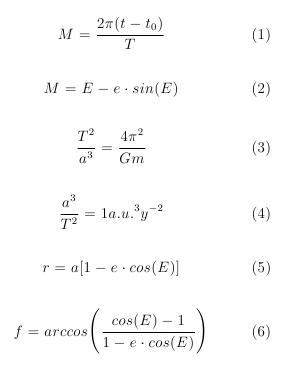
How to determine a body position along an orbit
We will answer on this question using an algorithmic form. First of all, let repeat what are known parameters. We have a and e as the parameters of the orbit. Let the central body be our Sun - which means that we know the mass m. It is requested to determine f and r in the moment t, knowing also the moment t0.
-
Calculate the orbital period T of the celestial body. For this purpose we will use the 3th Kepler's law. It holds (3) in general, while here we have (4).
-
Calculate the main anomaly M. Once we know T than we can calculate M using the equation (1).
-
Solve the Kepler's Equation. We can solve it numerically, following the next procedure.
1.step: E0=M
2.step: E1=M+esin(E0)
3.step: E2=M+esin(E1)
...
...to the desired accuracy.
4. Calculate r and f. Using relations (5) and (6) one can directly calculate orbital position vector r and true anomaly f.

Case studies
A comet orbiting the Sun
Calculate the orbital position vector r and the true anomaly f of a comet a year after the passage of periapsis. The orbit of the comet around the Sun is ellipse with major semi-axis a=4 a.u. and eccentricity e=0.66.
Solution: Firstly, we have to use the third Kepler law in order to calculate orbital period of the comet. Thus, a3/ P2= 1 au3y-2 → P2 = a3 / 1 au3y-2 = 64 y2 → P = 8 y. As the next step we can calculate the main anomaly by means of equation (1):
M = 2π(t - t0) / P = 2π(8 - 1) / 8 = 1.75π = 3150
Now we have to solve the relation (2), which can be done numerically:
E0 = 1.75π
E1= 1.75π + 0.66144 * sin(1.75π)
…
…
Usage of the relation (5) leads to
r = 4au * (1 – 0.66144 * cos(4.84) giving the result r = 3.65 astronomical units.
The true anomaly f will be calculated using the relation (6),
f = arccos{ [cos(4.84) – 0.66144] / [1 – 0.66144 * cos(4.84)] }
A short calculation gives the value of true anomaly f = 1250.
Position of the Halley's comet
Halley's comet approaches the Sun every 75.6 years. The last perihelion the comet passed in 1986 (9th February). The length of major semi-axis is 17.8 au while the eccentricity is 0.96. How far from the Sun the comet is currently?







