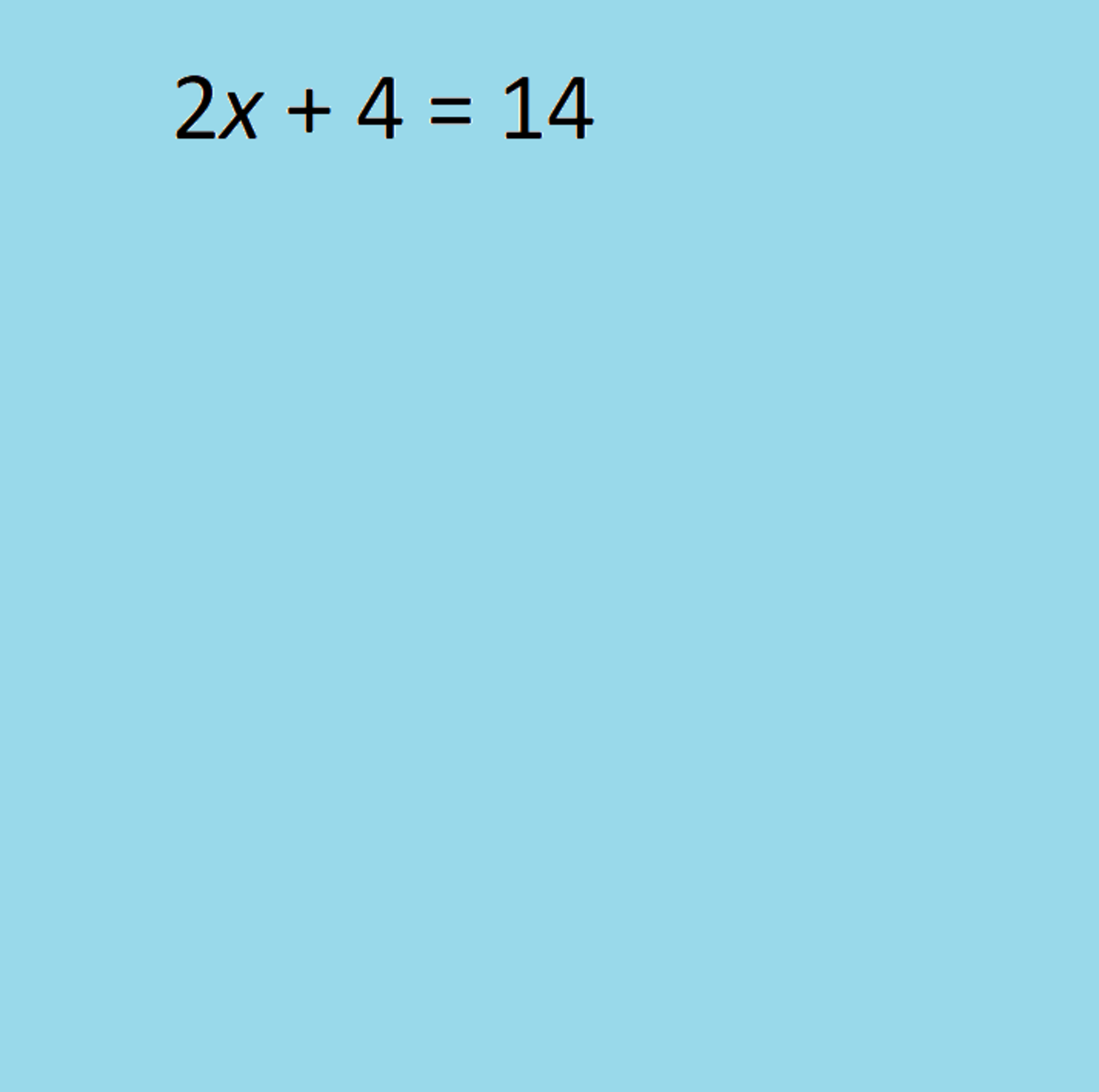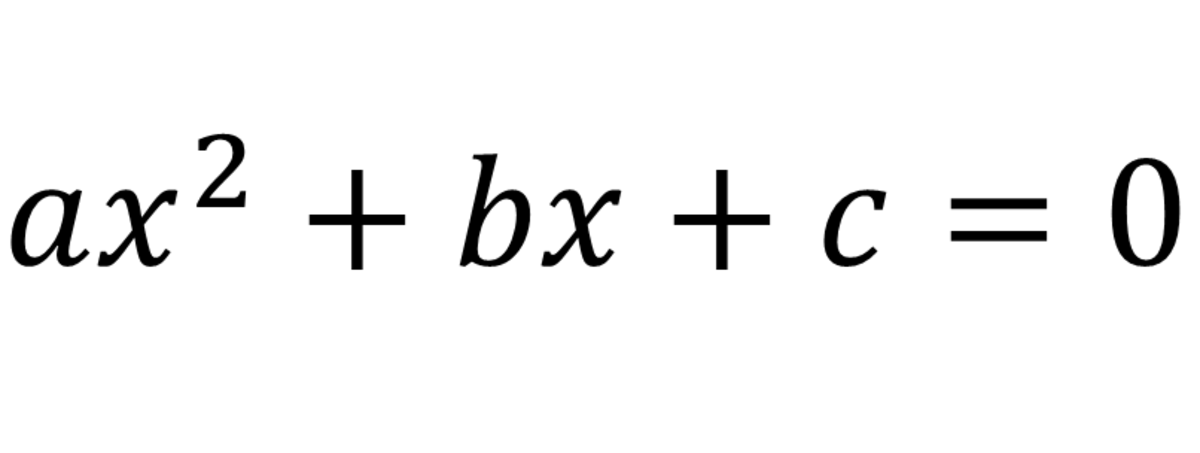LINEAR FUNCTION
THE LINEAR FUNCTION
The function f, defined by the first degree equation :
f = { ( X, Y)/ Y = mX + b } ;
where "m" and "b" are constants, is called a linear function. The function derives its name from the fact that its graph is a straight line.
The zero of a function is the X-value for which Y, the value of the function is zero. By
letting Y = 0 we can find the zero of a linear function by solving for X in the equation
mX + b = 0. Generally speaking, the zeros of a function are the roots or solution of the equarion f(X) = 0.
Review of Solving an Equation
In solving for an equation, we apply the following properties of equalities.
**Addition/Subtraction Properties:
The same number or algebraic expressions maybe added to or subtracted from both members of the equation.
**Multiplication/Division Properties
Both members of an equation maybe multiplied or divided by any nonzero number.
Illustration #1 :
4X - 5 = X + 7
+ 5 + 5
==============
4X = X + 12
- X -X
============
(1/3) 3 X = 12 (1/3)
X = 4
GRAPH OF A LINEAR FUNCTION
The graph of a linear function is a straight line. There are three methods of graphing a linear function or equation.
First, the table of values is employed.
Illustration #2 : Given the linear equation Y = 5X - 3
Assign first a certain value for X, then solve for Y.
Let X = 1, therefore Y = 5(1) - 3 = 2. Point (1, 2) is an ordered pair.
Then assign another value for X, let X = 2. Thus Y = 5(2) - 3 = 10 - 3 = 7
Point (2, 7 ) is another ordered pair. Now you can draw the graph of Y = 5X - 3
since you have two sets of ordered pairs for at least two points determine a line.
Plot now the points in the Cartesian Plane with points (1, 2) and (2,7)
The second method is known as the Slope-Intercept Method making use of the slope (m) and Y - intercept (b). Let us use this method this time to graph Y = 5X - 3.
The coefficient of X is the slope, in the given equation it is 5 and -3 is the Y-intercept.
Y-intercept is a point on the Y-axis where the graph crosses the Y-axis. The slope is the ratio of the rise to the run of the graph. The slope m = 5 indicates a ratio of 5:1. Plot first -3 on the Y-axis, from this point move five units up and then move one unit to the right.
Connect -3 to the endpoint which is (1,2).
The third method is known as the Intercept-Intercept Method which makes use of the X-intercept and the Y-intercept. Using the given equation Y = 5X - 3, let us use the Intercept-Intercept Method of graphing this.
Let X = 0 first then solve for Y;
Y = 5(0) - 3 Y = -3 thus (0, -3) is one ordered pair of the graph.
Then let Y = 0 and solve for X;
0 = 5X - 3
+3 +3
3 = 5X or (1/5) 5X = 3 (1/5)
X = 3/5
Therefore (3/5, 0) is another ordered pair. Plot these two points in the Cartesian Plane
Then connect them.
Illustration #3: Graph the equation Y = - 4X - 5
Using Slope-Intercept Method:
Plot -5 on the Y-axis.
Slope (m) = -4 ; rise = -4 and run = 1 or rise = 4 and run = -1.
Move 4 units up then move one unit left. It is left because its value is negative.
You can see that the graph is leaning to the left unlike the previous one, the graph is leaning to the right..Positive value for a slope reflects a graph which is leaning to the right. Negative value for slope refects a graph which is leaning to the left.
When the slope = 0, Y = b therefore the graph is one horizontal line, parallel to the X -axis.
Try to graph the following equations :
(1) 3Y = -2X + 6
- (2) 5Y = 10X - 7
(3) 4Y = 12
(4) 2Y = -5X - 8
- (5) 3X = 9