Logarithms

The logarithm of a number to a given base is the power or exponent to which the base must be raised in order to produce the number. Logarithms were invented by two men but separately. Napier invented his logarithms in 1614 with an algebraic approach. Burgi invented his logarithms in 1620 with a geometric approach. The objective of both men was to simplify mathematical calculations. Neither of those two men had a concept of a logarithmic base. The possibility of defining logarithms as exponents was recognized by John Wallis in 1685 and by Johann Bernoulli in 1694. Also it is important to mention that like multiplication is a shortcut for addition, logarithms are a shortcut for exponents.

Log _a b = c <==> a^c = b

- So as you can see, logarithms are a kind of shortcuts for exponents. In this logarithm a is the base;

- The base can’t be equal to one because 1 to the power of any number is equal to 1;

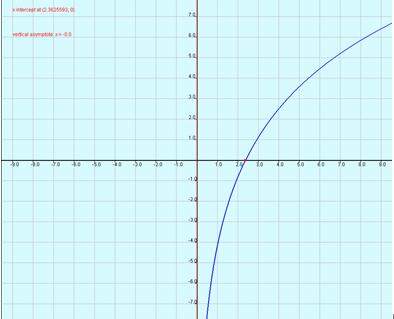
- It is also possible to make graphs out of these logarithms. There are two cases. The first case is if a>1 then the graph will look like "Graph 1", at the right.

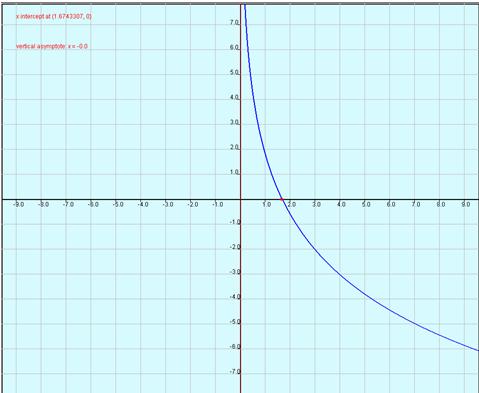
-the second case is when 0<a<1 then the graph looks like "Graph 2".

- The domain is R;

- The range is (0, +infinity)

Log_a 1= 0

-Every number is equal to 1 if you bring it to the power of 0;

Log_a a = 1

- Every number when brought to the power of 1 is equal to that number;

Log_a x/y = log_a x – log_a y

-if you have a fraction then the logarithm is equal to the logarithm of the numerator minus the logarithm of the denominator with the same base in both logarithms;

Log_a (x*y) = log_a x + log_a y

-if you have a fraction then the logarithm is equal to the logarithm of the numerator plus the logarithm of the denominator with the same base in both logarithms;

Log_a xⁿ = n*log_a x

-if you have an exponent then you can move that exponent in front og the logarithm multiplicating it all with 3;

Log_a x = log_b x / log_b a

-this rule is used when you for some reason need to change the base of the logarithm;

-Also logarithms can be:

• Common (logarithms with base 10)
• Natural (logarithms of base e)

• In chemistry
• In spectrometry and optics
• In psychophysics
• In computer science
• Musical intervals are measured logarithmically as semitones
• The Richter scale measures earthquake intensity on a base-10 logarithmic scale.
• In astronomy, the apparent magnitude measures the brightness of stars logarithmically, since the eye also responds logarithmically to brightness.
• In geometry the logarithm is used to form the metric for the half-plane model of hyperbolic geometry.