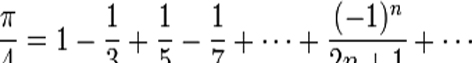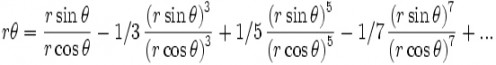MATHEMATICS IN MEDIEVAL INDIA: THE KERALA SCHOOL
MATHEMATICS IN MEDIEVAL INDIA: THE KERALA SCHOOL
The south Indian state of Kerala located at the tip of the Indian peninsula is well known as a tourist destination. But it has more to offer than scenic beauty and exotic history. Its contribution to mathematics and astronomy is slowly being recognized amongst scholars around the world. Its greatest contribution to this field were between the fourteenth and seventeenth centuries .
Many of their contributions, preceded discoveries in European mathematics by almost 200 years
The most prominent mathematicians of the Kerala School and their works were:
Nilakantha's Tantra Samgraha,
Jyesthadeva's Yuktibhasa,
Putumana Somayaji's Karana Paddhati
Sankara Varman' s Sadratnamala .
The Kerala schools contributions include:
The Gregory and Leibniz series for the inverse tangent,
The Leibniz power series for p,
Newton power series for the sine and cosine,
Rational approximations of trigonometric functions
Madhavan of Sangamagrama (c. 1340-1425)
He is credited to be the founder of the Kerala school. Though his work Karana Paddhati was supposed to have been written between 1375 and 1475, it is only through the works of later scholars we get to know him
Madhava's discoveries include
The Taylor series for the sine, cosine, tangent and arctangent functions;
The second-order and the third-order Taylor series approximations of the sine and cosine functions
The power series of π, now known as the Madhava-Leibniz series; Madhava correctly computed the value of π to 9 decimal placesand 13 decimal places, and produced sine and cosine tables to 9 decimal places of accuracy.
Narayanan Pandit
(1340-1400), His major works, are arithmetical treatise called Ganita Kaumudi and an algebraic treatise called Bijganita Vatamsa. His other work or Karma-Paddhati is a commentary of Bhaskara II’s Lilavathi. Narayanan’s major works contain a variety of mathematical developments and they are
A rule to calculate approximate values of square roots,
Investigations into the second order indeterminate equation nq2 + 1 = p2
Solutions of indeterminate higher-order equations
Mathematical operations with zero
Geometrical rules and a discussion of magic squares and similar figures.
Nilakanthan Somayaji (1444-1555) was an astronomer, but his Aryabhatiya Bhasya and Tantra Samgraha contain work on infinite-series expansions, problems of algebra and spherical geometry.
Nilakantha's most notable work however was Tantra Samgraha. He also wrote a commentary of ARYABHATIYA named Aryabhatiya-bhashya, His most significant contribution has been the derivation and proof of the Madhava-Gregory series for the arctangent trigonometric function where he used inductive mathematical proofs. He also gave sophisticated explanations of the irrationality of π, the correct formulation for the equation of the center of the planets, and a heliocentric model of the solar system.
Jyesthadeva (c. 1500)
Jyesthadeva wrote, in the regional language Malayalam and not Sanskrit. His work YUKTIBHASA contained detailed derivations of many theorems and formulae used in those times. . It contained most of the developments of earlier Kerala School mathematicians, particularly from Madhava Jyesthadevan also gave the earliest statement of Wallis theorem
The contributions of above mathematicians were two centuries before the invention of calculus in Europe. However, they did not formulate a systematic theory of differentiation and integration
Links
http://www-history.mcs.st-and.ac.uk/history/Biographies/Madhava.html
http://www-history.mcs.st-and.ac.uk/history/Biographies/Narayana.html
http://www-history.mcs.st-and.ac.uk/history/Biographies/Nilakantha.html
http://www-history.mcs.st-and.ac.uk/history/Biographies/Jyesthadeva.html
http://yuktibhasa.bestguide1.com/
http://www.nationmaster.com/encyclopedia/Yuktibhasa
http://india_resource.tripod.com/mathematics.htm
http://www.experiencefestival.com/history_of_calculus_-_controversy_newton_leibnitz_or_madhava
http://www-groups.dcs.st-andrews.ac.uk/~history/References/Madhava.html
http://www.jstor.org/pss/3620374
http://www.experiencefestival.com/indian_mathematician