Archimedes
Archimedes has been immortalised by the story that he discovered the Principle of Buoyancy (often called Archimedes’ Principle) while taking a bath, and ran naked from the bath shouting the words “Eureka”, which means “I’ve found it”. However, this was just one of the many scientific discoveries and contributions to mathematics made by Archimedes.
Archimedes is unquestionably recognised as the leading mathematician of antiquity. E. T. Bell in his Men of Mathematics has claimed that Archimedes was one of the three greatest mathematicians of all time – the others being Sir Isaac Newton (1642 – 1727) and Carl Friedrich Gauss (1777 – 1855). While some would regard Bell’s claim as fanciful, stating that it is impossible to compare intellects of quite different periods of history, there is no doubt that Archimedes was an exceptional genius.
Archimedes was of Greek heritage, but born in Syracuse, Sicily in around 287 BC. He was the son of an astronomer named Pheidias who was an aristocrat, and possibly related to the king of Syracuse, Hieron II. Archimedes lived for a time at the University of Alexandria where he befriended the mathematicians Eratosthenes, and Conon, amongst others.
Archimedes himself had some interest in astronomy and constructed a planetarium to portray the motions of the heavenly bodies. However, it was his inventions of mechanical contrivances and war machines – such as levers, catapults, pulleys, movable poles for dropping heavy weights on enemy ships and cranes with hooks to raise and smash enemy ships – that made him famous. It’s even claimed that he used giant magnifying glasses to set the enemy vessels on fire. After using a compound pulley to move a very heavy ship, Archimedes is reported to have said, “Give me a place to stand on and I will move the earth”.
However, Archimedes was a great thinker and placed far more importance on the product of his mind than he did on the value of these mechanical contrivances.
Altogether ten treatises of Archimedes have survived, three devoted to plane geometry – Measurement of a Circle , Quadrature of the Parabola and On spirals , two to three-dimensional geometry – On the Sphere and Cylinder and On Conoids and Spheroids , one on arithmetic – The Sand Reckoner , two on applied mathematics and a collection of works known as the Liber assumtorum .
The final work was simply called Method .
Archimedes wrote two books on applied mathematics that are still extant. The first was named On Plane Equilibriums in which he discussed methods to find the centroids (centres of gravity) of several plane figures. The second, named On Floating Bodies, was a fairly advanced work on hydrostatics. However, one statement, known as the Principal of Archimedes was undoubtedly put to practical use when King Hieron called on the help of Archimedes. The king suspected that a dishonest goldsmith had not used pure gold when making his crown, and asked for Archimedes’ help. The mathematician applied the following: ‘A solid heavier than a fluid will, if placed in it, descend to the bottom of the fluid, and the solid will, when weighed in the fluid, be lighter than its true weight by the weight of the fluid displaced.’ (Translation due to T L Heath in The Works of Archimedes .)
Archimedes also wrote a treatise named Method that was lost to the world until a copy was discovered by chance in 1906 in Constantinople. The Method was written in the form of a letter to Eratosthenes and describes ideas that foreshadowed the integral calculus. Archimedes used his method to find areas of geometrical shapes and volumes of solids.
These works of Archimedes are at such an advanced level of content and exposition that they exhibit many of the qualities of a modern journal article – originality, well-written using an economy of presentation, and rigour.
Archimedes was reportedly often so engrossed in what he was doing that he became oblivious to his surroundings, and this proved to be a contributing factor in his death. Archimedes died during the sacking of Syracuse in 212 BC. He was so preoccupied with a diagram he was drawing in the sand that, when a Roman soldier got in his way, he told the soldier to move on. The latter was so incensed that he ran his spear through the old mathematician and killed him.
A contribution of Archimedes to mathematics
Archimedes contributed so much to mathematics that it is difficult to isolate any one example. However, one of the easiest to visualise was the method he used to find an approximation for π using circumscribed and inscribed regular polygons of a circle. This appears as Proposition 3 of Measurement of a Circle. What follows is a simplified version of what Archimedes did.
Archimedes started with a circle of unit radius:
(What the unit used was is not important. It could be 1 inch, or 1 centimetre, or 1 anything. The important thing is that all lengths will be measured using the same unit.)
He then inscribed a regular hexagon inside the circle:

By comparing the circumference of the circle with the perimeter of the hexagon, he concluded that π > 3
Next, he inscribed a regular dodecagon inside the circle:

Again by comparing the circumference of the circle with the perimeter of the dodecagon, he concluded that π > 3 1/10(or more precisely 3.10597)
He then doubled the number of sides of the regular polygon to 24, then 48, then 96; each time obtaining better and better approximations for π. Using this method, he concluded that π > 3 10/71 (or 3.140845 as a rounded decimal).
Archimedes then repeated the whole process, but this time using circumscribed regular polygons:
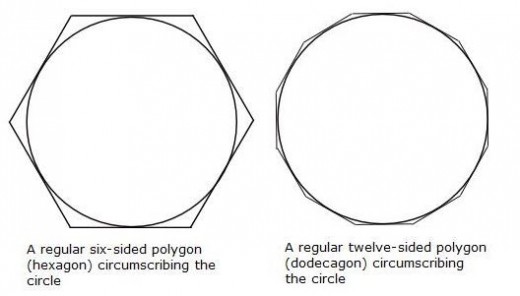
By following a similar method, comparing the circumference of the circle with the perimeters of regular polygons with 6, 12, 24, 48 and eventually 96 sides, he concluded that π < 3 1/7 (or 3.142857 as a rounded decimal).
Taking the two results together, Archimedes gave the result that
3 10/71 < π < 3 1/7
This was a remarkably accurate result for its time.