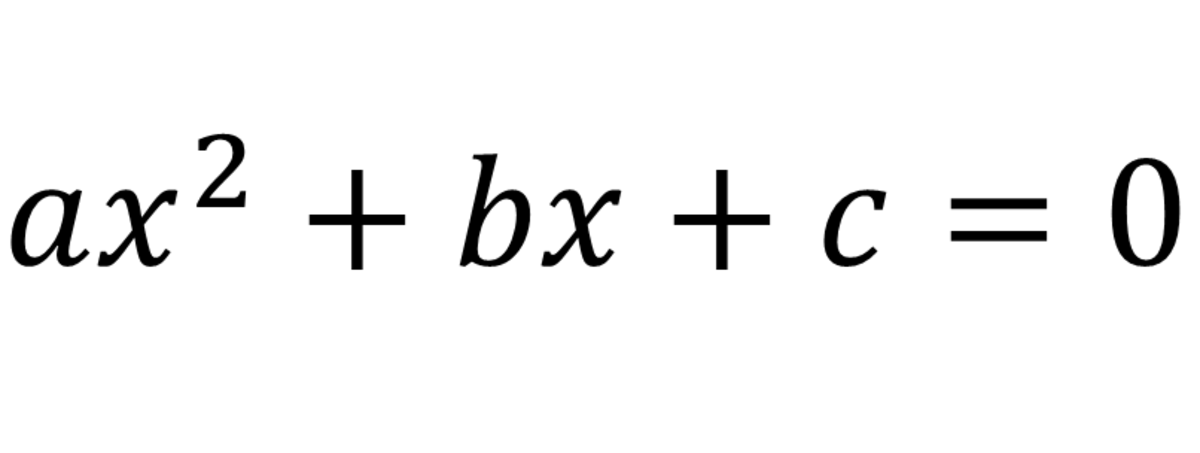Girolamo Cardano

Bastard, heretic, gambler, occultist, astrologer, alchemist, father of a murderer, plagiarist, committer of suicide, great mathematician and inventor, Cardano was a man of genius.

Girolamo Cardano was born in Pavia, Italy in 1501, the illegitimate son of a lawyer from Milano. He is also known by the variants Gerolamo and Geronimo, and often by the anglicised version of his surname, Cardan.

Cardano trained and practised as a doctor, but had a passion for mathematics which he studied in his spare time. He travelled widely, even going as far as Scotland to tend to the Archbishop of St, Andrews who was afflicted with asthma. He is credited by some as the first to describe typhoid fever.

He was undoubtedly one of the most gifted mathematicians of the sixteenth century and held the chairs of mathematics at Pavia, Bologna and Milano.

Cardano has been portrayed by history as a wicked man. It is rumoured that he was so angry with one of his sons one day that he cut off the boy’s ears. His other son was executed for murdering his wife. He also had an interest in astrology. When he published a horoscope of the life of Christ, he was imprisoned for heresy. But later he was appointed as an astrologer at the papal court. He used astrology to predict the date of his own death (21^st September 1576) and, it is said, committed suicide so that his prediction would come true. He also wrote a book on gambling, Liber de ludo aleae (written in1526, but published posthumously), which led to the development of the elementary rules of probability. Cardano’s breaking of his promise to Tartaglia not to publish the solution of the general cubic equation is further evidence that Cardano was not of good character.

Besides mathematics, Cardano wrote on a number of other subjects, including medicine, astronomy, physics, alchemy, music, and he published two encyclopaedias of natural science. These include details of a number of Cardano’s inventions. He even wrote an autobiography, De vita propria, in 1576.His most important scientific work was his De subtilitate rerum , a philosophical treatise on Aristotelian physics, but including some new discoveries from his own time.

In 1539 he published a work on arithmetic entitled Practica arithmetice et mensurandi singularis . One topic discussed in this work was the rationalisation of the denominator of an expression containing cube roots.

But it was Cardano’s writing on algebra which distinguished him as one of the foremost mathematicians of his time. His greatest work was the treatise Artis magnae, sive de regulis algebraicis , usually referred to as Ars Magna, and published in 1545. This work was of such importance that the year 1545 is often considered to be the beginning of the modern era of mathematics. Ars Magna not only contains the controversial method for solving the cubic equation, but also a solution of the general quartic (degree 4) equation which was first discovered by his assistant Ludovico Ferrari (1522-1565), and an approximate method for obtaining the roots of an equation of any degree. Cardano allows for irrational and negative roots of an equation and even hints at the possibility of imaginary roots and the existence of complex numbers.

The most enduring contribution of this work to mathematics was not the mechanical solution of cubic and quartic equations. These methods were cumbersome and did little to supersede approximate methods of solution that were already well known. No, the work was important for another reason - it led to the study of polynomials of any order and in particular a search for the solution of the general quintic (degree 5) equation. It was to be another 279 years before Niels Henrik Abel showed that such a solution does not exist.

One contribution of Cardano to mathematics that is fairly easy to understand is known today as Descartes Rule of Signs, incorrectly attributed to René Descartes (1596-1650).

Cardano used syncopated algebra and was unable to express the rule concisely. Throughout this discussion, I will use modern notation

Cardano was well aware that a polynomial of degree n has n roots. This may in some cases include repeated roots, but the number is always n. Take, for example, a polynomial like f(x) = 5x - 7x³ - 2x² - 4x⁵ + 1

Since the highest power of x is x⁵,this has degree 5, and therefore f(x) = 0 has 5 roots. But how many of them are positive and how many are negative? The Rule of Signs helps answer this question.

First rewrite the polynomial in correct order of terms from highest to lowest:

f(x) = -4x⁵ - 7x³ - 2x² + 5x + 1

Positive Roots

Count how many times the sign changes in the polynomial.

The signs are - - - + and +

So the sign changes from - to +. That’s 1 change of sign.

The number of times the sign changes tells us the maximum number of positive roots of f(x) = 0

The equation -4x⁵ - 7x³ - 2x² + 5x + 1 = 0, therefore, has a maximum of 1 positive root.

Negative Roots

Replace x by -x in the polynomial:

-4(-x)⁵ - 7(-x)³ - 2(-x)² + 5(-x) + 1

= 4x⁵ + 7x³ - 2x²- 5x + 1

Count how many times the sign changes in the polynomial.

The signs are + + - - and +

So the sign changes from + to - to +. That’s 2 changes of sign.

The number of times the sign changes tells us the maximum number of negative roots of f(x) = 0

The equation -4x⁵ - 7x³ + 2x² + 5x + 1 = 0, therefore, has a maximum of 2 negative roots.

It seems that the problem is solved - there is 1 positive root and 2 negative roots. But there should be 5 roots altogether. What about the other 2 roots? Cardano recognised that the other two roots are complex (although he did not use that name - he dismissed them as ‘sophistic’), and he recognised that complex roots always occur in pairs. This was a mark of his genius.

The Rule of Signs, therefore, tells us there are two possibilities:

The equation -4x⁵ - 7x³ - 2x² + 5x + 1 = 0 could have 1 positive root, 2 negative roots and 2 complex roots, or it could have 1 positive root, 0 negative roots and 4 complex roots. In fact the first possibility is true in this case.