Tartaglia
Tartaglia was one of the most colourful characters in the History of Mathematics.
Born Niccolò Fontana in the northern Italian town of Brescia in around 1499, he was given the name Tartaglia (which means ‘stammerer’ in Italian) following an incident in 1512 that left him with a lifetime imperfection of speech.
In 1512 Brescia was invaded by the French. Niccolò and other inhabitants of Brescia sought sanctuary in the cathedral, but the French soldiers pursued them and many of the people were massacred. Over 45,000 residents of Brescia were killed. Niccolò’s father, Michele Fontana, was one of those killed, and the boy was badly injured with a split skull and a sabre cut that passed through his jaw and palate. This resulted in the speech impediment that led to his name Tartaglia.
With the death of Michele, the family became impoverished. Tartaglia’s mother sent him to school for a few days, but could not afford to pay for regular schooling. So the boy stole a book, from which he taught himself to read and write.
That Tartaglia taught himself not only to read and write, but how to use and apply mathematics, is a mark of his genius.
He lectured at Verona before being appointed to the chair of mathematics at Venice in 1535.
Among Tartaglia’s most significant achievements were his translations into Italian of works of Archimedes and Euclid; in particular the1543 translation of Book V of Euclid’s Elements. Tartaglia used a Latin translation of the original Greek, rather than the commonly used Arabic translations that contained some inaccuracies, especially in relation to the Eudoxus’ Theory of proportions. Tartaglia’s commentary on this theory was later used by Galileo.
Tartaglia’s works include Nova Scienza (1537) in which he investigated the fall of bodies under gravity, Inventioni (1546) which contains among other things his solution of the cubic equation, an arithmetic treatise Trattato de numeri e misuri (1556), and a two volume treatise on arithmetic, published in 1560. In this he developed a method to obtain binomial coefficients using a triangle similar to Pascal's Triangle,
Tartaglia also applied mathematics to the science of artillery fire, and adapted Heron’s formula for the area of a triangle to give an expression for the volume of a tetrahedron given the lengths of its sides - Tartaglia’s Formula.
By Tartaglia’s time, the solution to the general quadratic equation ax2 + bx + c = 0 was well known. In modern notation we give the solutions in the form of the Quadratic Equation Formula:
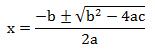
Tartaglia’s most memorable achievement was his contribution to the solution of the general cubic equation ax3 + bx2 + cx + d = 0.
As stepping stones on the way to solving the general cubic equation, mathematicians tacked two simpler cases:
Case 1: x3 + mx = n where the coefficient of x2 is zero and
Case 2: x3 + px2 = n where the coefficient of x is zero.
Case 1 was successfully solved in 1515 by Scipione del Ferro, professor of mathematics at Bologna University. Del Ferro did not publish his result, but shared his discovery with his pupil Antonio Fior.
In 1535 Tartaglia announced that he had solved Case 2. However, Fior did not believe Tartaglia had a solution and challenged him to a public contest to solve cubic equations. Taking up the challenge, Tartaglia set himself the task of solving Case 1 also, which he did before the contest. Having solved both types, Tartaglia easily won the contest against Fior.
Later Tartaglia shared his solutions with Girolamo Cardano who promised not to publish. However, when Cardano learned of del Ferro’s earlier solution of Case 1, he decided to publish the solutions in his famous treatise Ars Magna, including Tartaglia’s solution of Case 2. This was followed by an acrimonious dispute between Tartaglia and Cardano.
Tartaglia died in Venice in 1557.
A contribution of Tartaglia to mathematics
In modern notation, Tartaglia gave the following solution to a cubic equation of the type
x3 + mx = n (Case 1 above):
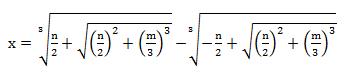
Example Solve the cubic equation x3 + 9x = 6
In this case m = 9 and n = 6
Therefore

Of course a cubic equation always has three solutions, but in this case the other two solutions are complex numbers.