Methods for Converting Recurring Decimals into Fractions
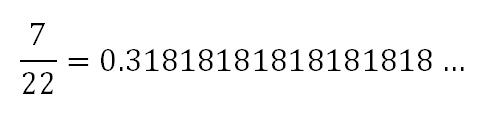
Methods for Converting Recurring Decimals into Fractions
A decimal form of a number is said to become recurring if at any point it becomes repeated indefinitely.
Keying 1 / 3 into a calculator will give 0.3333333333... which is a recurring decimal.
Keying 1 / 12 into a calculator will give 0.0833333.... which is also a recurring decimal.
The 3s on the end of both of these numbers actually continue forever and are limited only by the number of digits on the calculator. These examples only involve 1 repeating digit, but as shown below, they may have more than 1 repeating digit.
0.9 recurring (0.9999..) is actually equal to 1, and a simple proof of this is shown in Section 3 of this article.
Section 1: The sum of an infinite geometric series
We will start by representing our recurring (or repeating) decimal as a (geometric) series. A geometric series is defined as a series with a constant ratio between successive terms.
For example:
X = 0.111111...
X = 0.1 + 0.01 + 0.001 + 0.0001 + 0.00001 + ... = 0.111...
X = 1 / 10 + 1 / 100 + 1/ 1000 + 1/10000 + ... = 0.111....
We have now created a series to represent 0.111.... We can write this as
X = a1 + a2 + a3 + a4 + a5 + ... + ak
In the example above, the ratio between the terms is 1 / 10, which we will call r. How this is derived is shown below.
Setting term a1 = 0.1, term a2 = 0.01 as above, it is clear that
1 / 10 * a1 = a2
1 / 10 * 0.1 = 0.01
We can see this continues with any successive terms we choose:
a5 = 0.00001, a6 = 0.000001
1 / 10 * a5 = a6
1 / 10 * 0.00001 = 0.000001
This shows that the recurrence relation looks like this:
r * an = an+1
And for this example:
1 / 10 * an = an+1
Using our ratio r = 1/10, we can simplify much further to:
a1 + a1r + a1r2+ a1r3+ a1r4 + ... + a1rn = 0.11111...
where
a1 = 0.1
a2 = a1r = 0.1*0.1 = 0.01
a3 = a1r2 = 0.1*0.01 = 0.001
ak = a1rn where n = k - 1.
This result can be proven for when the recurrence relationship has this form, but it is not detailed here as it is rather more complicated.
Summing the geometric series: Derivation of the formula
Now, using we can derive a formula which will allow us to calculate the value of this series as a fraction:
Let S(n) = a1 + a1r + a1r2+ a1r3+ a1r4 + ... + a1rn
Then r.S(n) = a1r + a1r2+ a1r3+ a1r4 + a1r5 ... + a1rn+1 (using . for simple multiplication here instead of * or x)
Then S(n) - r.S(n) = ( 1 - r ).S(n) = a1 - a1r + a1r - a1r2 + a1r2 - ... - a1rn + a1rn - a1rn+1
All terms cancel apart from a1 and - a1rn+1 giving:
(1-r).S(n) = a1- a1rn+1
S(n) = ( a1- a1rn+1 ) / ( 1 - r )
As n → ∞ (as n approaches infinity) to include the infinite terms in the series we constructed with our recurring decimal, the term a1rn+1 will approach 0 as -1 < r < 1 and therefore a1rn+1will become more and more negligible compared to other terms when raised to a larger and larger powers, n, and can therefore be ignored giving:
S(n) = a1 / ( 1 - r )
Some information on limits can be found on another page: http://hubpages.com/hub/Limits-in-Mathematics
-1 < r < 1 or equivalently |r| < 1 (absolute value) is necessary to give convergence of this series as values of r with absolute value larger than 1 will result in larger and larger terms for n > 1, and therefore will sum to infinity.
If we now go back to the simple example of X = 1 / 9 = 0.111... using the formula with the first term in the series we constructed from the decimal expansion of X, a1 = 0.1, and r = 0.1.
S(n) = 0.1 / (1 - 0.1) = 0.1 / 0.9 = 1 / 9
And a slightly more difficult example:
X = 0.3181818181818...
We must take the 0.3 out of the series to start with as it does not repeat:
X = 0.3 + 0.018181818...... = 0.3 + 18 / 1000 + 18 / 100000 + 18 / 10000000 + ....
X = 0.3 + a1 + a1r + a1r2+ a1r3+ a1r4 + ... + a1rnwhere a1 = 18 / 1000, and r = 1/100
We apply the formula S(n) = a1 / ( 1 - r ) to the last part of X
X = 0.3 + [S(n)] = 0.3 + [ ( 18 / 1000 ) / ( 1 - ( 1 / 100 ) ) ] = 0.3 + [ ( 18 / 1000 ) / ( 99 / 100 ) ]
Simplyfying of the S(n) term gives:
X = 0.3 + [ 18 / 990 ]
X = 0.3 + [ 1 / 55 ]
X = 3 / 10 + 1 / 55 = 33 / 110 + 2 / 110 = 35 / 110
X = 7 / 22
Section 2: Simultaneous equations
There is a also a way to obtain fractions from recurring decimals using algebra and simultaneous equations.
Example 1
X = 0.111111... (1)
We wish to set up a second equation such that the repeating part after the decimal is 'aligned' with the first equation, so that when we subtract them from each other it is eliminated.
We however need to shift this second in some direction in order for (2) - (1) to be non-zero. The easiest way to do this is multiply the first equation by 10 to give the second.
10X = 1.1111... (2)
Now calculating (2) - (1)
10X - X = 1.1111... - 0.1111..
9X = 1
X = 1/9
Example 2
X = 0.3181818181818...
We need to use different equations this time as the number does not start repeating until after the 0.3 which requires a shift of 1 digit, therefore multiplication of X by 101 needs to be done to give equation (1). This can be extended to a general rule where equation (1) = 10a X to give a left shift of a digits:
10X = 3.1818181818... (1)
(In the earlier example this multiplication of X to set up equation (1) was not necessary as it started repeating immediately after the decimal point.)
It then starts to repeat every 2 digits, so a second 'aligned' equation can be easily set up by multiplying the first equation by 102. This can again be extended to a general rule where if it starts repeating every b digits, then you will multiply the first equation by 10b. Or equation (2) = 10a10bX
1000X = 318.18181818.... (2)
Calculating (2) - (1):
1000X - 10X = 318.1818181... - 3.181818181...
990X = 315
X = 315 / 990
X = 7 / 22
Section 3: Showing that 0.9 recurring is equal to 1 (0.99999... = 1)
The recurring decimal 0.99999... can be shown to equal 1 in a number of ways, two of these are listed below. A proof can be constructed using the epsilon-delta method or the completeness theorem, although this is more closely related to the idea of Limits.
This may come as a surprise to some, who may believe 0.99999... is less than 1. A simplified example for why this is not the case, is as follows:
You are asked to draw a mark showing 0.99999...cm on a ruler. You may initially imagine drawing the mark as close to left of 1cm as possible, in order for it to be just less than 1cm, but this would mean there would be gap between your mark and the 1cm mark. This gap can then be measured (albeit with very accurate equipment and a microscope) to give a measurement we shall call x.
This means that we require 1 - x = 0.99999..., so suppose our original gap was 0.1cm, we would get 1 - 0.1 = 0.9cm, which is less than 0.99999... cm
We could then decrease our gap to 0.01cm to attempt to get closer to 0.99999...cm, this would give us 1 - 0.01 = 0.99cm, which is still less than 0.99999...cm
We can then imagine decreasing our gap even further to 0.001cm, this would give us 1- 0.001 = 0.999cm, which is still less than 0.99999...cm etc.
It quickly becomes clear that no matter how small we choose the gap between the mark for 1cm and the mark for 0.99999...cm, it will always be too big. Therefore we can conclude the only correct place to put the line is exactly on the mark for 1cm.
Method 1: Using the formula for an infinite geometric series with |r| < 1
S(n) = a1 / ( 1 - r )
Recall that a1 is our first term, and r is the ratio between the successive terms as in previous examples.
S(n) = 0.99999...
This can be broken down into the below geometric series, where a1 = 0.9, a2 = 0.9r, a3 = 0.9r2, a4 = 0.9r4...etc
giving:
S(n) = 0.9 + 0.09 + 0.009 + 0.0009 + 0.00009 + ...
So we see that a1 = 0.9 and r = 0.1, and put these values into our formula:
S(n) = 0.9 / ( 1 - 0.1)
S(n) = 0.9 / 0.9
S(n) = 1.
We can see the result of our sum is 1, and as there are infinity successive terms in our series S(n), we can conclude 0.99999... is exactly equal to 1 in the same way as we concluded the recurring decimals in the previous examples were exactly equal to their respective fraction forms.
Method 2: Using simultaneous equations
X = 0.99999... (1)
10X = 9.99999... (2)
Then take (2) - (1) as in previous examples
10X - X = 9
9X = 9
X = 1.
Related articles by the same author:
Absolute Value
Irrational Numbers