Natural Constants: G and e

Part of an overview of the physics and mathematics pertaining to naturally occurring constants. In this chapter: G and e.

The Gravity Constant
Gravity: seven-time Oscar winner, gyroscopic space adventure and respiratory fiesta; also, a force keeping us glued to Earth. If you have not yet learned how gravity works, now is the time to take the leap. First, a brief primer before introducing the gravitational constant.
The story of our understanding of gravity begins with Johannes Kepler, a German mathematician and astronomer. Kepler formulated three laws governing the motion of celestial bodies based on previous astronomical observations. Though inspired by similar hypotheses, his laws were the first to provide a valid argument against the geo-centric universal model, which claimed that all celestial bodies orbited Earth. More on Kepler’s laws in a moment….

Isaac Newtown had already observed that some force existed which draws objects to Earth’s surface; additionally, he noted that this force is equal to the product of the object’s mass and its acceleration. Furthermore, when a body (or object) exerts a force on another body, the body also receives a force from the other object -- more commonly explained by the famed line “every action has an equal and opposite reaction.” Lastly, Newton observed that when a moving object (and it should be noted that an object such as your computer is moving with Earth’s rotation) is viewed from an inertial frame -- a perspective that moves at a constant velocity -- that object will be moving with constant velocity unless a force is exerted on the object. These three important observations came to be known as Newton’s three laws of motion -- though not in the order described -- and explain the general mechanics of bodies in motion.
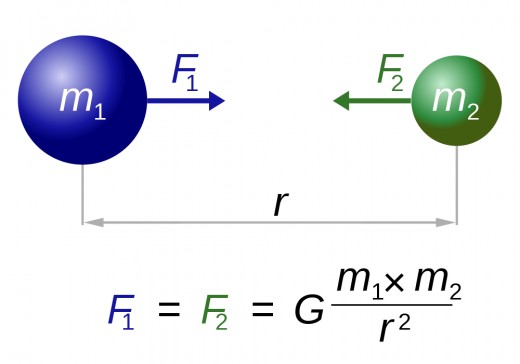
Derivation of G
Using these laws, Newton analyzed the behavior of many bodies including planets. Now, back to Kepler: Newton further analyzed the laws of planetary motion by reconciling his and Kepler’s laws. By investigating the force Earth exerted on small objects, he concluded that the motion is based on force by two masses, Earth and the object. This motivated the idea of gravity and the understanding of planetary motion as that based on a two-mass system. Deriving Kepler’s laws using his own, Newton concluded that the force observed was proportional -- but not equal to -- the product of the masses and inversely proportional to the square of the distance between them: . Moreover, he calculated that this proportionality was linear, so that the two sides of the proportionality relate by a constant: (G for gravity).
This gravitational constant G, found to equal approximately 6.67384 × 10-11 m3 kg-1 s-2 in SI units, governs the gravitational behavior of our known universe and explains planetary motion as well as the vertical motion of every object on Earth. G’s mystical value remains constant in any circumstance and hugely simplifies the analysis of interactions between bodies.



Euler's Number and Natural Logarithms
Euler’s number is one of the most mysteriously reappearing numbers in natural science, economics and mathematics. Though the constant is most commonly written e to honor Leonard Euler, the number was discovered by Johann Bernoulli in an attempt to better understand exponential growth. In his classic example of compounding interest, Bernoulli found that compounding some amount of interest on a principle balance n times during a year shows an increase in the year-end balance as n increases. As n approaches infinity, the account balance increase approaches roughly 2.71828 times its principle. This was an interesting, though seemingly insignificant finding. However, following this discovery, Bernoulli started noticing the number popping up in probability problems and mathematical applications such as calculus. First, however, came the natural logarithm, ln.
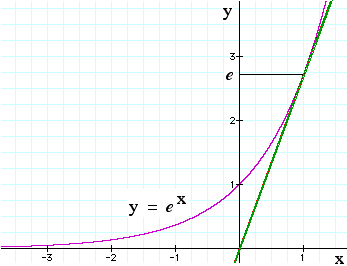
ln
Logarithms, in general, are transformations that relate exponential and linear functions. By definition, all logarithmic functions have a value of zero when the dependent variable is equal to 1, and have approach minus infinity as the dependent variable approaches zero from the positive. The natural logarithm is a special case of logarithms that also has a logarithmic slope of 1 at 0, when the dependent is equal to 1. Remember all of Bernoulli’s coincidental findings of e? Hold on tight…. Suppose that the natural log of some number equals 1 [ln(x) = 1], what is x? The results, obtained experimentally and graphically, were conclusive that x = e. Furthermore, if we consider the equation ex = e we can easily see that x must be 1, but we can also utilize the natural logarithm and rules of logarithmic calculation to get ln(ex) = x, for any x. This powerful relationship between e and ln is still commonly used today and is extremely useful in calculus.
Calculus
Both e and ln are hugely useful in calculus namely because of the aforementioned logarithmic slope of the natural logarithm. Revision and ironing out of the exact nature of natural logarithms has led to their calculus definition, that d/dx [ln(x)] = 1/x and from that the general definition has been derived for e that d/dx [ex] = integral [ex ] = ex. The discovery of these simple relationships is an extremely powerful tool in many prominent fields of mathematics, but is especially utilized in logarithmic differentiation and integration.

Arrhenius Type Equations
Euler’s number extends far beyond mathematics, which makes it such an important constant. Svante Arrhenius, a Swedish physicist, mathematician, chemist, etc., discovered what we now term the Arrhenius relationship. By his proposal, temperature-dependent reactions (corrosion, diffusion, creep, evaporation and fusion to name a few) can be accurately analyzed with the relationship Y = Yoe(Q/RT), where Y is the reaction product, Yo is the initial condition, Q is the energy of reaction, R the gas constant (sometimes the Boltzmann constant is used instead for correct unit conversion), and T is the temperature. This e-based relationship is ubiquitous and greatly clarifying in otherwise cryptic reaction processes. However, these equations are still difficult to solve -- without ln that is. The natural logarithm makes the solution trivial and further crystallizes its relationship with and importance of Euler's number.
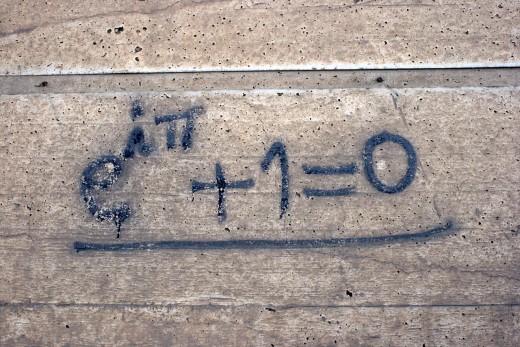
Just for fun.

More to Come
The intention of this series is to cover all of the natural, physical and mathematical constants. Of course, pi will receive its own hub, as will c0(speed of light). The number 23 will also receive an honorable mention. Stay tuned.
-sehrm