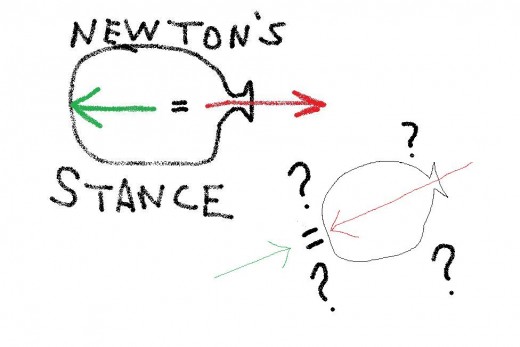
Mikel's third law of motion:

For every action there is an opposite and equal re-action.

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

" No amount of experimentation can ever prove me right; a single experiment can prove me wrong." Albert Einstein

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

It is not possible for there to be an "equal and opposite" re-action for every action. What there are, are "consequences" for every action, and or non-action. Consequences that may or may not be equal and opposite.

An example of this law is what happens if we step off of a small boat onto the bank of a lake: as we move in the direction of the shore, the boat tends to move in the opposite direction. If the boat is very small when we push against it, it will shoot away from us. A demonstration that the force returned was not equal, is the consequence of us falling into the water. This disproves Newton's theory, so long as the amount of force the person is exerting against the very small boat, is an amount great enough to propel them to the shore (and counter the effects of gravity) if an equal amount of force is returned. Again since the reactionary force is less than the initial force, the person falls in the lake.

In the time it takes for the forces to interact there is a split second where the forces are equal and opposite, but after that split second the forces are UN-equal and may or may not be opposite. It is in that instant that motion is achieved. If one force is not greater than the other motion will not be attained. The forces are NOT equal and opposite for anything more than the split second it takes for the greater force to overpower the lesser force, and attain motion.

Part of Newton's flaw is in the assumption that every object has the capacity to return an infinite amount of force.

Small objects such as pebbles floating in space do not have an infinite amount of force to draw on. A man floating in space can exert a force on a floating pebble and send the pebble flying away without much or any reactionary force acting on the man. The fact that the pebble goes flying away and the man does not, is proof that Newton's third law is flawed.

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

Mikel's third law of motion:

For every action (or non-action) there will be some kind of consequence. A consequence that may or may not be equal and opposite. Motion is possible because the involved forces are not equal and opposite. When the involved forces are equal and opposite motion cannot be attained.

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

'Q' said:

"A gross misunderstanding of Newtons third law on Mikel's part is the problem here.

F=ma

F is the force

m is the mass

a is the acceleration

If the mass fluctuates, as in the difference in mass between the man and the pebble, the acceleration must also fluctuate proportionally to the mass.

The boat example is even more flawed as Mikel fails to take into consideration friction."

Mikel says:

F=ma is the second law not the third.

The third laws equation is F= -F every time. Which of course is incorrect and proven false every time anything achieves motion. If F=MA of a football lineman and f=ma of a toddler the toddler's force equation will be less than that of the lineman, therefore F does not equal -F (with the situation being the lineman and toddler are pushing against each other). The smaller mass and acceleration of the toddler will result in a smaller -F than that of the lineman, therefore the forces will not be equal. Newton states they must always be equal, Newton and you are incorrect.

The mathematical expression Newton ascribes as the Third Law can only ever equal 0 and be correct. The only number in existence that can be both Equal and Opposite is '0'.

Zero is the only possible correct answer to the equation F=-F.

*The Emperor's new suit...

I think being afraid of being the only smart person in the room that didn't see how the third law was true, when everyone else evidently understood it, kept many smart people from saying anything. In my opinion what Newton describes in his third law is Stagnation.

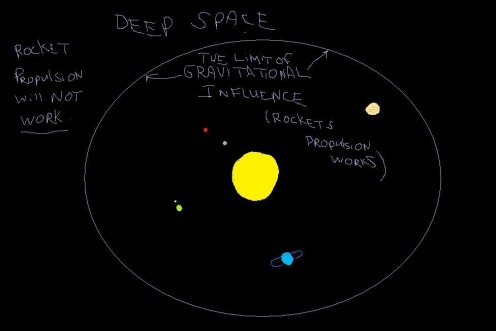
I further believe that as humanity branches out into deep space we will discover our propulsion systems won't function as we now believe they will. I think the failure of rocket propulsion in deep space will permanently prove my stance on the laws of motion.

The effects of the huge gravitational forces in our solar system are what allow our propulsion systems to work in space, and that is why it seems like Newton was correct. But about this he wasn't correct and neither are some of the theories about black holes... Holes in Space?