Noether's Theorem: Symmetry in Nature
Noether's Theorem (also called The Noether Theorem) is a theorem discovered by mathematician Emmy Noether. It is extremely useful in many areas of theoretical physics, and is frequently used in classical and quantum field theory to predict the conservation laws that must be obeyed in all processes, such as the conservation of energy.
What is Noether's Theorem?
Expressed in words, Noether's Theorem says:
"For every continuous symmetry, there are corresponding quantities whose values are conserved."


What is Symmetry?
The easiest way to understand symmetry is with an example. Consider the pattern on a butterfly's wings. The pattern is completely symmetrical - the butterfly's left wing is the exact mirror image of the right wing. If you flipped an image of the butterfly over in a mirror, swapping left with right, it would look exactly the same as the original. This means that the butterfly has a reflection symmetry.
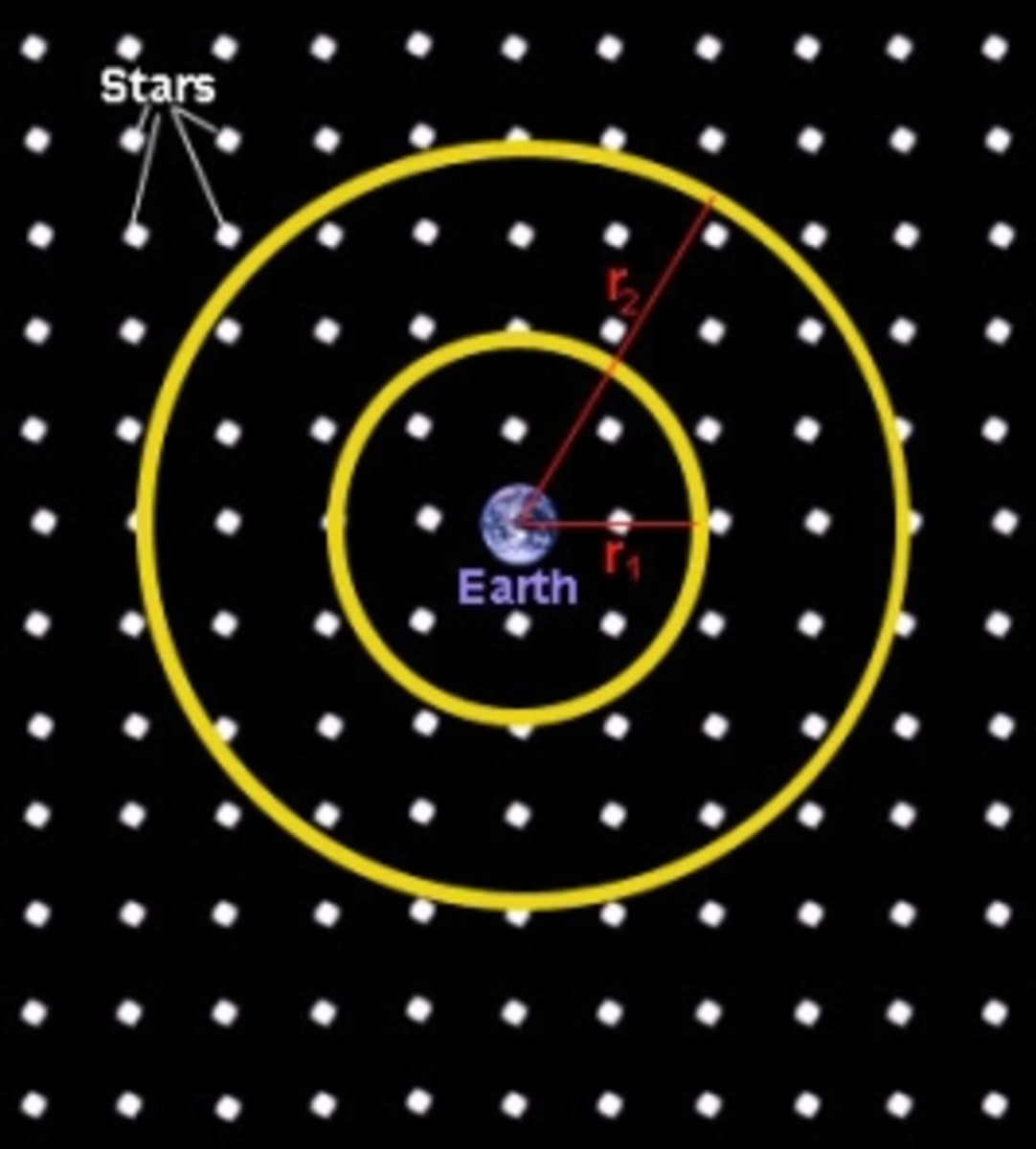
That's one type of symmetry, and is the kind that most people refer to when they say something is symmetrical. But there are also other kinds. Consider the star shown in the picture. It has rotational symmetry, because you can rotate it by 72 degrees and it will look exactly the same as it did before the rotation. Because you can do this 5 times until you get back to where you started, we say the star has rotational symmetry order 5.
The universe also has rotational symmetry. What that means is that if you do an experiment, and then you rotate all your apparatus and do the same experiment again, you will always get the same result. It's like the image of the star looking the same after it has been rotated by 72 degrees, but with one difference: the universe doesn't care how many degrees you rotate by, the result will be the same regardless. Rotating the universe is more like rotating a circle than a star - no matter how many degrees you rotate by, everything looks the same. The universe has continuous rotational symmetry.
From Noether's theorem, we know that there is a conservation law associated with this symmetry. It turns out that the continuous rotational symmetry of the universe leads to the law that angular momentum is always conserved. Put simply, this means that if you have a bicycle wheel spinning freely, with no frictional forces acting on it, the wheel will continue to spin at exactly the same speed forever. It's angular momentum will be conserved.
Read ngriffin360's hub on conservation of angular momentum.
The universe also has time symmetry, which means that the outcome of an experiment is not affected by when the experiment is performed - i.e. if you do an experiment today, and do the same experiment next Tuesday, being careful to keep all the variables the same, you should expect the same result. This symmetry leads to the conservation of energy.
There is also translation symmetry - if you do an experiment in one place, and then relocate your laboratory ten miles south of where you are now, then again you should get the same results (ignoring local effects due to variations in the Earth's gravitational field etc). This symmetry leads to the conservation of momentum.
The mathematics needed to prove Noether's Theorem and to show how each symmetry leads to its conservation law can be found in any of the following maths books. The proof isn't very long, but you need to know calculus to follow it.
Emmy Noether's Wonderful Theorem - for UK Amazon users
topquark works as a researcher in theoretical particle physics and blogs about science at The Particle Pen.