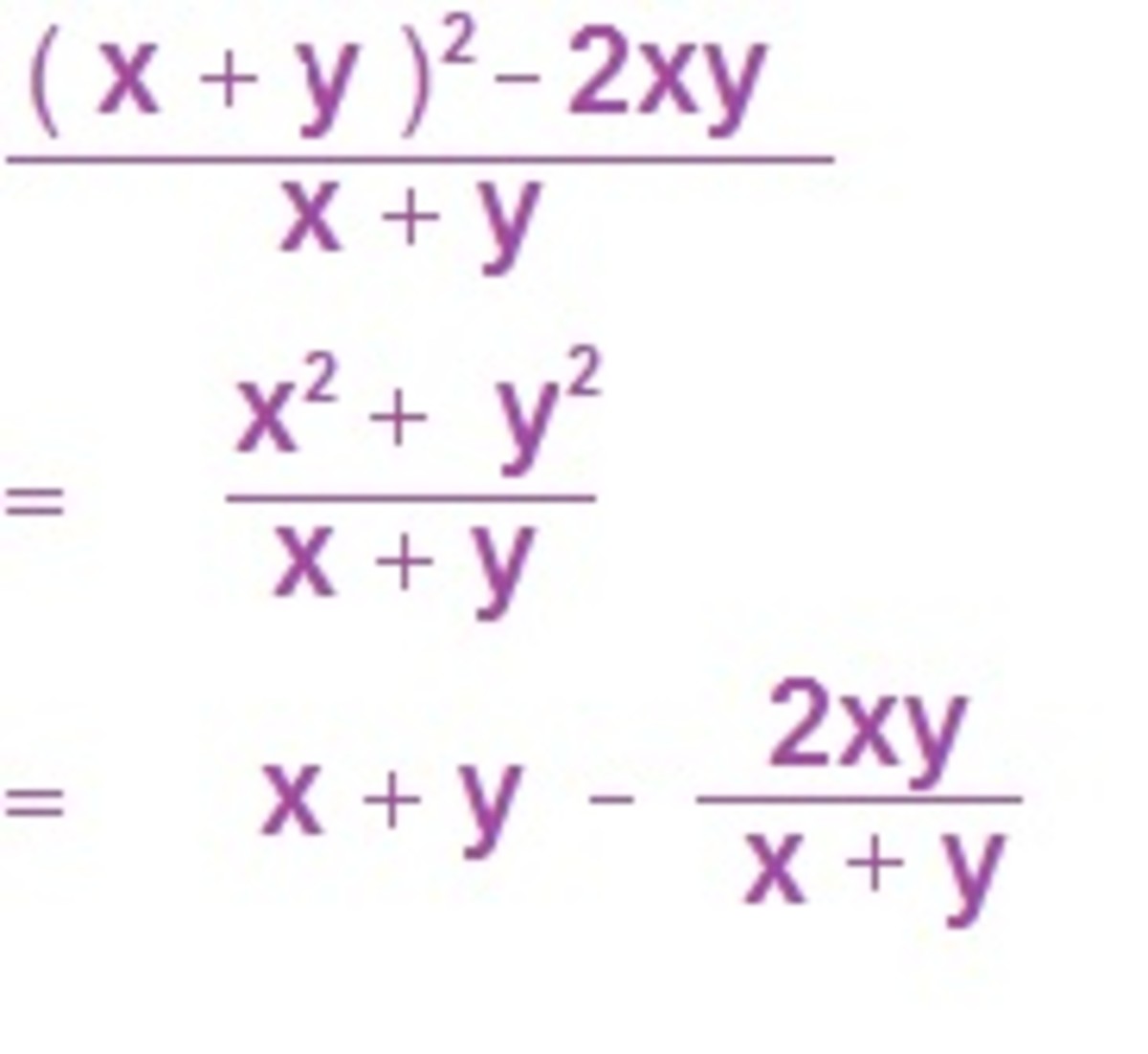Numbers Are Beautiful

Some people hate numbers, yet we cannot very well get along without them. If you attempt to teach a new, numeric trick to someone who considers "numbers" an enemy, you might more easily haul them in for dental surgery. Yes, it is that painful to them.
But try having a checking account without numbers. And if some checkout clerk "accidentally" pockets the change that should have been yours, how do you know without thinking about numbers? Or if you win the lottery, what do all those zeros mean? Aren't they beautiful? And yet, there is a big difference between 0.00000001 and 10,000,000.0, even though they have the same number of zeros.
Here There Be Symbols
Every "advanced" civilization has had some way of keeping track of numbers. This goes along with language and writing. It is part of the basics. And not all systems are based on ten.
The Babylonians used a base-60 set of numerals written in cuneiform in soft clay, later hardened in the sun to create a lasting record. Base-60 merely means that there are 59 characters representing individual numeric values, with 60 represented by a "1" and a "0," if the system had one, or possibly a blank. Like the characters "1" through "9" in the decimal system (base ten), the Babylonians had characters for "1" through "59" in their sexagesimal system.

These digits were inherited from the Sumerian and Akkadian civilizations, but unlike their systems, the Babylonian proved to be a positional system. This was an important advance, because a positional system allows the reader to know the magnitude of each digit. For instance, in our decimal system, the character "3" in the numbers 3, 30, 300, and 3000, have the magnitudes of "units," "tens," "hundreds," and "thousands," respectively. This conceptual breakthrough greatly aided in the art of calculations. And the Babylonians were famous for their astronomical observations and the calculations based on them, aided by the abacus, which was first seen in this region.
Why a base-60 system? No one knows for certain, but an interesting fact attached to "60" is that it is the smallest number evenly divisible by all of the whole numbers up to 6. It is also evenly divisible by 10, 12, 15, 20 and 30.
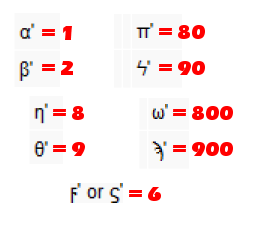
Other cultures, like the Greeks and the Hebrews, used letters from their alphabet as numeric symbols. The Ionic (Greek) alphabetic number system, adopted in the fourth century BC, used letters of the alphabet, combined with a diacritic character (like an accent) to distinguish numerals from letters. Letters used in this manner represented separate values for all units (1-9), tens (10-90), and hundreds (100-900), thus requiring 27 separate symbols. Because the Greek alphabet possessed only 24 symbols, the character set was extended with 3 obsolete letters (digamma or sometimes stigma for 6, qoppa for 90, and sampi for 900).
The Romans, however, did not use letters of their alphabet, as is commonly thought. They likely used notches on a stick for counting, like the tally sticks used in Europe up into the nineteenth century. The simple vertical "I" represented "one." Two notches joined together at one end signified a different magnitude of number, so what we picture as "V" represented "5." A still higher magnitude of number was symbolized by two notches joined in the middle so that "X" indicated "10." The "V" on its side becomes the rounded "C" signifying "100." And two inverted "V's" joined at the bottom become "M" for "1000."
Have you ever tried calculations with Roman numerals? There is a method to it, but it proves far more complicated than calculations with our modern "Arabic" system.

What might have happened if some Roman mathematician had realized how cumbersome were the symbols for their numbers. Such a paradigm shift would not have changed human nature. It would not have eliminated the greed and corruption which decayed the Empire from the inside out. Still, it is interesting to consider what might have happened. What would such a change have done to history, if anything.
Old Khmer (Cambodian) numerals include the first material evidence of zero used in a positional decimal system. The Khmer civilization of the seventh century thus had a more sophisticated numeral system than that of the Romans, and its days of empire would not arrive for yet another two hundred years.

The Maya numerals were based on a pattern of dots and dashes in a vigesimal (base-20) system. This included a shell symbol for zero. Numbers above 19 were created by vertical arrangements of the first 20 symbols, stacked in powers of 20 (20, 400, 8000, and so on). With all of their calculations, the Mayans predicted that we would experience the turning of an age on December 21, 2012.
What we traditionally call "Arabic" numerals were originated farther east, in India. The North African Arabs who introduced the numeral system to Europe in the Middle Ages, called the system Hindu numerals after their earlier source. As we all know, these decimal numerals consist of 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. In order to produce numbers of larger value, one merely places a symbol to the left of the unit value. Each position is based on powers of ten (the value of the base). Thus following 1, the numbers 10, 100 and 1000 are each ten times the previous value.

The Incredible Nothing
Zero. Yes, it is beautiful—so round and clean and empty.
Add zero to any number and you get your original number. Like glass, it is completely transparent during addition.
Any number times zero has a product of zero. Doesn't that look like magic? Aim a zero at any other number and that number disappears during multiplication.
Raise any number to the zero power and you always get 1. Don't know about exponents? We will come back to them, shortly.
In fractions, any number with a zero in the numerator (the quantity on top of the fraction bar), gives us a value of zero, no matter what the denominator (the quantity below the fraction bar). For example (0 / 3,492,769,107) is numerically equivalent to (0 / 1).
However, if you have a zero in the denominator (remember, below the bar), you get something mathematicians like to call "undefined." In some computer programs, you might occasionally get a "divide by zero" error (the programmer should have taken care of that bug). But I like to think of this as "infinity." I suppose a few mathematicians out there will groan with dissatisfaction, but symbolically, I don't see why we can't use any number divided by zero as a symbol for infinity. There is a certain round and wonderful simplicity to it, and the idea is not without some merit. Think about it for a moment. If you take a fraction and make the denominator (bottom) smaller and smaller, approaching zero, while keeping the numerator (top) constant (say "42"), the value of the entire fraction gets larger and larger, approaching infinity. Of course, infinity is not a specific numeric value. It's sort of the opposite of zero, not only in quantity, but also specificity.
And, as mathematicians will tell you, no number times zero will result in one. Normally, if you both divide a number by a specific quantity and multiply by that same quantity, you get the original number. It is as if you had multiplied by one. For example, if you divide 84 by 42 and then multiply by 42, you get the original number — (84 / 42) x 42 = 84 x 1 = 84. If we remember our math, we know that 42/42 = 1. Alas, zero defies this. Try (84 / 0) x 0 = undefined.
So, what is this quantity (0 / 0)? Is the value zero or infinity? Or both? Or because both numerator and denominator are the same, is the value one? Or is it simply "undefined?" Or does this point out a deeper relationship between zero, one and infinity?
A few years ago, when I was taking calculus in college, the professor graphed on the blackboard the derivative of one function and the image of it has stuck in my mind. What is a "derivative?" Glad you asked. Calculus is all about rates of change and measuring changes. A derivative is about the instantaneous rate of change at a particular moment in a series of changes. For instance, when you drop an object, it accelerates toward the ground. It starts at zero velocity and picks up speed, moment by moment. At any one moment, the object has a very specific velocity. The next moment, that velocity has increased. The derivative of the function of gravitational acceleration is a velocity at some specific moment in time.
The graph that stuck with me showed a line at the X-axis with a hole (a discontinuity) at X = 0. Where X = 0, the Y-value was ±∞ (plus-or-minus infinity)—as far from zero as one can get. The image of it still gives me goose bumps. Why? Because I had made a few discoveries, years earlier, about the mechanics of creation. If X is a measure of ego, and Y is a measure of power over physical reality, then this graph would indicate zero power over the universe at any value of ego other than zero, and infinite power over physical reality at zero ego. My father called this state, "neutral affinity" for its emotional neutrality (neither desiring nor fearing).
To go from a state of nothing to a state of all-powerful with no intervening steps or gradation should not be all that foreign to us. After all, a woman can be either pregnant or not, but nothing in between; there is no such thing as being "half pregnant."
More such spiritual aspects can be found at The Love of God website.
Which Century is Your Computer From?
Have you ever wondered why living in the twenty-first century (21) contains years beginning with "20" rather than "21?" Most of us grew up in the twentieth century (20) which contained years beginning with "19." It has to do with the rather simple convention that we do not call the first century (containing all the years less than 100) the "zeroeth" century. It remains the "first" century, because we like beginning our counting with one rather than zero. So, the second century contained all years from 101 to 200. Ah, there's the "2," right at the end of the sequence.
In computer programming, however, it is typical to begin counting with zero, not one. Frequently programmers find bugs in their software of the "off-by-one" kind because of this. They can sometimes forget to subtract one from the count. For instance, the thirtieth item (item #30) in a whole number count starting from zero is actually the one valued "29."
Computers do not inherently use the decimal system. When it seems to speak decimal to us, it is only after translating numbers into our own system. In fact, computers think of everything in its own system — binary. The computer's numeric system is base-2 — ones and zeros. All computer instructions are ones and zeros. Even the alphabet and punctuation are ones and zeroes to the computer. Let me show you how it works.
Base-2 contains two kinds of digits — "0" and "1." Compare this to our Base-ten system which contains ten kinds of digits — "0" through "9."
Counting in binary is simple. You start with 0, then 1, and next — because we have now used up our set of symbols— we place a "1" to the left of the "units" place, just as we do when we go past "9" in the decimal system. Just as ten is "10" in decimal, two is "10" in binary. Confused? Hold on; it gets better.
Decimal numbers and binary equivalents:
0 = 0
1 = 1
2 = 10
3 = 11
4 = 100
5 = 101
6 = 110
7 = 111
8 = 1000
Notice the pattern? You always add one to the units position and carry over, just as you do in the decimal system. When you get to 9 in the decimal system, adding 1 means that you carry a 1 over into the next position to the left (the tens position), and replace the 9 with a zero.
Letters and punctuation are stored in a computer as series of ones and zeros. The American Standard Code for Information Interchange (ASCII) defines the capital letter "A" as binary "1000001." Capital "Z" is binary "1011010." Lowercase "a" is binary "1100001," and lower case "z" is binary "1111010." In fact, though the computer performs numeric calculations using its own native binary, it displays numeric symbols for us humans using for "0" the binary "110000," and for "9" the binary "111001."
Looking at all those ones and zeros can be a bit mind-numbing, so computers translate binary into its own second language. And no, this is not decimal. The computer's second language is hexadecimal — base-16. Why? Because translation is so easy. Base-16 uses sixteen symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E and F.
Decimal, binary and hexadecimal equivalents:
2 = 10 = 2
4 = 100 = 4
8 = 1000 = 8
16 = 10000 = 10 (see the relationship between binary and hexadecimal?)
32 = 100000 = 20
256 = 100000000 = 100
You might note that 256 is equal to 16 x 16. Just as ten times ten (10 x 10) equals one hundred (100) in decimal, sixteen times sixteen (10 x 10) equals two hundred and fifty six (100) in hexadecimal.
How Bright it Is
Stars are beautiful to look at, especially on a clear, moonless night far from the city lights. This is how the ancients saw them—up close and personal.
The magnitude scale marks the brightness of individual stars. For some unfamiliar with astronomy, this scale takes some getting used to. We are all familiar with the survey questions which begin, "On a scale from one to ten, ten being best,..." but stellar magnitudes seem counterintuitive. Instead of the larger numbers representing the brighter stars, the smaller numbers represent greater brightness.
The reasoning is simple. Think of it as a scale of importance. Who wouldn't want to be number one, instead of number ten or number one thousand? To the ancients, the brightest stars in the night sky were of the "first" magnitude. Bright stars with a little less vigor were "second" magnitude. Dim stars at the edge of visibility were "sixth" magnitude. Another way of looking at it is as a place winner in the Olympics—first place (the gold) is much better than third (the bronze).
Modern astronomical science has set the difference of five magnitudes at precisely one hundred times in brightness. The difference in one magnitude thus proves to be the fifth root of one hundred, or approximately 2.5119.
Stars brighter than "first" magnitude are given zero or negative numbers. Venus, at its brightest, shines at magnitude –4.9, while our full Moon has a magnitude of –12.9 and Sol, our sun, shines with a magnitude –26.74.
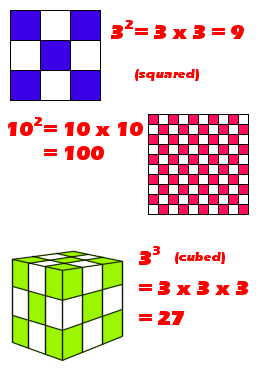
Packaging Numbers to do Powerful Work
The beginning of this article displays a picture of Albert Einstein with his most famous equation, E = mc2. That little "2" at the end is usually read "squared." This is an exponent which simply means that the quantity is multiplied by itself. In the case of his famous equation, this means E = m x c x c, where "E" stands for energy, "m" stands for mass, and "c" stands for the velocity of light (186,282 miles per second). So, c-squared is 186,282 times 186,282, which equals 34,700,983,524 miles-squared per second-squared.
Why do we use the word "square?" Imagine for a moment looking at square tiles on the floor. Count three tiles in one direction and then from the same starting point, count three more tiles at right angles to the first three. Now, consider these as the top and side of a larger square. How many smaller squares make up that larger square? The answer is, quite simply, the length of one side times the length of the other, or 3 x 3. The number of smaller squares is, of course, nine. Thus, three squared equals nine. Squaring a number has a visual relationship with physical area.
This talk of shapes extends into the third dimension. When we say that a number is cubed, the picture of it is similarly simple. For instance, three cubed (33) is merely 3 x 3 x 3, which equals 27. If you were to count the smaller cubes in a larger cube of 3 along an edge, their number would be 27.
Larger exponents—also called "higher powers"—don't have such fancy names as "squared" or "cubed." An exponent of "4" is merely stated as "to the fourth power." And so exponents 5, 6, and 7 would be stated, "to the fifth power," "to the sixth power," and "to the seventh power." Quite often, the word "power" is left off, so that 34 can be stated, "three to the fourth."
Three to the seventh (37) equals 3 x 3 x 3 x 3 x 3 x 3 x 3. Count the number of threes and you will see that there are seven of them. If you are curious, three to the seventh power is equivalent to 2,187, which has no great significance other than being the value in our example.
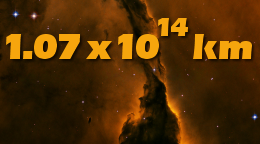
Scientists use exponents all the time. Perhaps they use exponents most frequently with something called "scientific notation." This is a way of writing numbers in a compact, easy-to-read format. Take the number, 107,000,000,000,000, for instance. At a glance, it is hard to understand—hard to assess immediately the value or magnitude. Scientists have created a format which moves the decimal point to the left, near the most significant digits, and then multiplies that number times ten raised to some exponent. This example is equivalent to 1.07 x 1014. The ten raised to the fourteenth power tells us just how far the decimal point has been moved. This tells us the magnitude of the number.
The number 100 would then equal 1.0 x 102. The number 33 would equal 3.3 x 101. And the number 0.007 would equal 7.0 x 10–3.
What is interesting about exponents is that they do not always have to be whole numbers. For instance 100.30103 (ten raised to the 0.30103 power) is approximately equal to 2. This fractional exponent is called the logarithm of 2. Strictly speaking, it is the logarithm (or "log") in base-10 of the number 2. The actual log10 (log to the base-10)of 2 cannot be written in its entirety, because it is not a simple fraction. Even at 32 significant digits, 0.30102999566398119521373889472449 is still only an approximation of the log10 of 2.
Computer programs have been written which draw very realistically waves on water, clouds in the sky, or leaves on a tree. The algorithms which describe these shapes create objects which have fractional dimensions—in other words, fractional exponents. Just as ten squared (102) describes two dimensions, or area, and ten cubed (103) describes three dimensions, or volume, fractional dimensions describe shapes which partially fill two, three or even four dimensions.
Not all logarithms are base-10. When science studies biological growth, population expansion or even rates of nuclear decay, the natural logarithm comes in handy. Natural logs are to the base-e. The constant called, "e," has a value of approximately 2.71828.
If you ever need the base-10 log of a number, but your calculator only has natural logs (sometimes written ln or loge), do not worry. Simply divide the natural log of the desired number by the natural log of ten.
For example, ln(2)/ln(10) = 0.30103, which is the correct answer for our base-10 log of 2. If you have a Windows-based computer, then your operating system comes with a handy calculator. This calculator has a standard (simple) mode and a scientific mode. If you switch to "scientific" mode, you will see a great many more buttons, including "log" and "ln." Simply type a "2," click the "ln" key, click the "/" (divide by) key, type "10," click the "ln" key again, then click the "=" (equals) key. This gives you the rather long answer which can usually be shortened to six or seven significant digits—0.3010300.
One other convenient fact about exponents is that multiplying two numbers is as simple as adding exponents. Dividing two numbers would involved subtracting exponents.
For instance, 2 x 4 = 100.30103 x 100.60206 = 100.90309 = 8. And notice that the last exponent, 0.90309 is the sum of the first two exponents. Ten raised to this fractional power is 8. Or to put it another way, 0.90309 is the base-10 log of 8.
And, of course, 32 x 36 = 38. In this example, it is easy to see that, with exponents, one is counting threes: (3 x 3) x (3 x 3 x 3 x 3 x 3 x 3) = (3 x 3 x 3 x 3 x 3 x 3 x 3 x 3).
The pattern of numbers—10, 100, 1000, and so on—in any base can be expressed as increasing exponents of that base. For example, in base-2, the numbers 1, 10, 100, 1000, and 10,000 are equivalent to 20, 21, 22, 23, and 24. Likewise, in base-10, the same numeric symbols are equivalent to 100, 101, 102, 103, and 104. Patterns like these make numbers very useful.

To the Stars
One practical example of scientific notation involves the distances to other stars. If we start with our own star—our sun—we have a distance of 93,000,000 miles from Earth. This would be written as 9.3 x 107 miles. The distance to Proxima Centauri (our closest neighbor, and part of the Alpha Centauri, 3-sun system) is about 2.47 x 1013 miles away.
The Andromeda galaxy (M31) is about 1.47 x 1019 miles from Earth, far enough away that its light takes 2.5 million years to make the trip. M31 is similar to our own Milky Way galaxy in size and shape and is part of the Local Group of galaxies.
Given that there are about 100 billion galaxies in the universe and that each galaxy may have up to 100 billion stars, on average, then the universe contains something like 1022 stars, with a modest percentage likely having planets. Somewhere out there, there may be other civilizations pondering numbers just as we have.
For more about stars, check out Ancient Suns Blog. For 3D astronomy space software, check out my Space Software website.
The Land of Numbers and Mathematics
What's your favorite numeric system?
© 2010 Rod Martin Jr