Phi: The World’s Most Remarkable Number
The golden ratio, also known as “phi,” (pronounced with a long i̅ sound) has intrigued Western intellectuals in numerous disciplines for at least 2400 years. According to author, Mario Livio, in The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number:
Some of the greatest mathematical minds of all ages, from Pythagoras and Euclid in ancient Greece, through the medieval Italian mathematician Leonardo of Pisa and the Renaissance astronomer Johannes Kepler, to present-day scientific figures such as Oxford physicist Roger Penrose, have spent endless hours over the simple ratio and its properties. But the fascination with the Golden Ratio is not confined to just mathematicians. Biologists, artists, musicians, historians, architects, psychologists, and even mystics have pondered and debated the basis of its ubiquity and appeal. In fact, it is probably fair to say that the Golden Ratio has inspired thinkers of all disciplines like no other number in the history of mathematics.
Why is this ancient number so important and does it still have relevance in the twenty-first century? The answer is an emphatic Yes, because the golden ratio has a perpetual link to mathematics, “the language of the universe.”
How Did Phi Acquire Its Name?
Phi’s history, from the origins of its name to its present-day use, from architecture to contemporary medicine, will provide the most propitious information to support its importance. Herein you will find an abridged history of its discovery.
Around 450 BC, a Greek sculptor name Phidias appears to have been the first person who used the Greek letter that now symbolizes phi. But it was not until approximately 1909, or the early 20th century, thousands of years later, that an American mathematician named Mark Barr proposed using the first letters in Phidias’ name to represent the golden ratio. And since that time, the golden ratio, or phi, has been symbolized by this Greek letter, or other corresponding names, including the “divine proportion.”
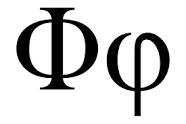
Mathematician Mark Barr
proposed using the first letter in the
name of Greek sculptor Phidias,
phi, to symbolize the golden ratio.
Usually, the lowercase form (φ) is
used. Sometimes, the uppercase
form (Φ) is used for the reciprocal
of the golden ratio, 1/φ.
Phi Has Other Names
Long before this astonishing number was first used, around 323-283 BC, after the death of Alexander the Great, Ptolemy I established the first university in Alexandria (known then as the Museum). Euclid, a Greek mathematician, sometimes called Euclid of Alexandria, and often referred to as the “Father of Geometry,” was in the first staff of teachers.
Euclid is the author of the best known book in the history of mathematics, The Elements, in which he attempted to comprehensively document all the mathematical knowledge of his time. “He contributed many new proofs, totally rearranged the contents attributed by others, to entire volumes, and designed the whole book.” It served as the main textbook for teaching mathematics, especially geometry, from its time of publication until the late 19th or early 20th century.
The Golden Ratio appears in The Elements in several places, but Euclid’s use of the golden ratio to construct the pentagon serves to highlight its relevance.
It All Starts With a Line
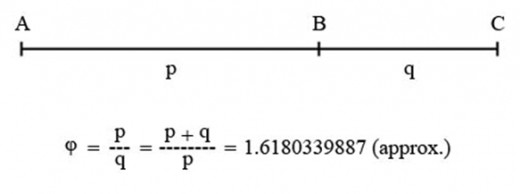
According to Mario Livio, to explain why the Golden Ratio is important for the construction of the pentagon, first, examine Figure 24, below. In this figure, the line AB is divided by point C. Euclid’s definition in Book VI of The Elements, which describes extreme and mean ratio, is such that: (larger segment)/(shorter segment) is equal to (whole line)/(larger segment). In other words, in Figure 24:
AC/CB=AB/AC.
How is this line division related to the pentagon? In a triangle n=3, and the sum of all angles is equal to 180 degrees. Every angle of the pentagon is therefore equal to 540/5=108 degrees. Imagine now that we draw two adjacent diagonals in the pentagon, as in Figure 25a, thus forming three isosceles (with two equal sides) triangles. Since the two angles near the base of an isosceles triangle are equal, the base angles in the two triangles on the sides are 36 degrees each [half of (180°-108°]. We, therefore, obtain for the angles of the middle triangle the values 36-72-72 (as marked on Figure 25a).

If we bisect one of the two 72-degree base angles (as in Figure 25b), we obtain a smaller triangle DBC with the same angles (36-72-72) as the large one ADB. Using very elementary geometry, according to Euclid’s definition, point C divides the line AB precisely in a Golden Ratio. Furthermore, the ratio of AD to DB is also equal to the Golden Ratio. (A short proof is given in Appendix 4). In other words, in a regular pentagon, the ratio of the diagonal to the side is equal to ɸ. This fact, according to Livio, illustrates that the ability to construct a line divided in a Golden Ratio provides at the same time a simple means of constructing the regular pentagon.
The ancient Greeks first studied phi because of its frequent appearance in geometry. But their fascination with the Golden Ratio was due, primarily, to its ability to construct the pentagon.

What is the Value of Phi?
Determining the precise value of ɸ will help us understand some unique algebraic properties associated with it. These properties were significant in helping the Golden Ratio rise to the “almost reverential status” that it eventually achieved.
Examine Figure 24, again, and take the length of the shorter segment, CB, to be 1 unit and the length of the longer one, AC, to be x units. If the ratio of x to 1 is the same as that of x +1 (length of the line AB) to x, then the line has been cut in extreme and mean ratio. We can solve for the value, x, of the Golden Ratio. From the definition of extreme and mean ratio:
x÷1=x+1÷x
Multiplying both sides by x, we get X² =x+1, or the simple quadratic equation:
X²-x-1=0.
Appendix 5 presents a reminder for how to solve a quadratic equation.

The two solutions of the equation for the Golden Ratio are:
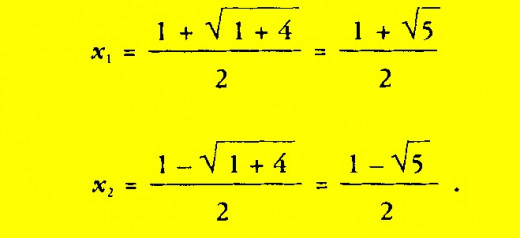
The positive solution ( ) 1.6180339887…. gives the value of the Golden Ratio. This demonstrates that ɸ is an irrational number since it is simply half the sum of 1 and the square root of 5. (Irrational numbers are numbers that can be written as decimals but not as fractions.)
The number ɸ also has some interesting properties. While the square of the number 1.6180339887… gives 2.6180339887…, its reciprocal (“one over phi”) gives 0.6180339887…., all having precisely the same digits after the decimal point.
Take a simple scientific pocket calculator and enter the number 1.6180339887 and hit the X² button. Do you see something surprising? The Golden Ratio has the unique property that you produce its square by simple adding the number 1, or 2.6180339887…, and its reciprocal (“one over”) by subtracting the number 1, or 0.6180339887.
The Pisa Connection
Another intriguing mathematical concept that correlates with the Golden Ratio emerged with Leonardo of Pisa, also known as Leonardo Fibonacci, the first important European mathematician. The first use of his nickname Fibonacci (from the Latin filius Bonacci, son of the Bonacci family, or (“son of good nature”) is traced to Italian mathematicians at the end of the eighteenth century.
Fibonacci’s story began in Pisa, Italy, best known today for its famous leaning bell tower, on which construction began during his youth. At that time, Pisa was a busy port city where goods from different continents were transported, sold and dispersed throughout parts of Italy, Sicily and Sardinia. They included spices, like salt, goatskins, wine and oil.

As the public clerks or merchants listed prices in Roman numerals and added them up on an abacus, Fibonacci watched intently. “As long as the medieval merchants stuck to simple addition and subtraction, they could get by with Roman numerals.” For example, to obtain the sum of 3,786 and 3,843, you would need to add MMMDCCLXXXVI to MMMDCCCXLIII.
ROMAN NUMERAL VALUES:
M=1000
D =500
C =100
L =50
X =10
V = 5
I = 1
Fibonacci witnessed the difficulty of using multiplication, which was a burdensome process. The primary mathematical application that was non-existent at the time was the place-value system, where a number written as 547 really means (5x10²) + (4x10¹) + (7x10°). Without it, the Western Europeans relied on the abacus.
The name “abacus” may have originated from avaq, the Hebrew word for dust, since the earliest of these calculation devices were simply boards dusted with sand, on which numbers could be traced.
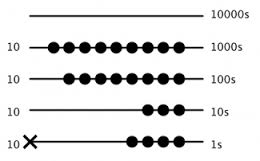
Fibonacci and the Abacus
The early abacus, during Fibonacci’s time, had counters sliding along different wires which “played the role of place value.”
A typical abacus had four wires, with beads on the bottom wire, representing units, those on the one above it, tens, those on the third, hundreds, and those on the top wire representing thousands. For simple arithmetic, the abacus was fairly efficient, but it presented significant disadvantages when it came to more complex computations.
Fibonacci was able to gain a greater understanding of the challenges faced with the antiquated mathematical system, on his tours of the Mediterranean with his father. Subsequently, in 1202, he decided to publish his first and best known book, Liber abaci, which means “The Book of Calculation,” although it has also been translated as “The Book of the Abacus,” in error. "The book’s intent was to describe more efficient methods of doing calculations without the use of an abacus". It was one of the most important books on mathematics in the Middle Ages, introducing Arabic numerals and methods throughout Europe.
Fibonacci and the New Math
In the book, Fibonacci provided the translation from Roman numerals to the “new math,” an introduction to the Hindu-Arabic number system that we use today, which included the nine Indian figures: 9 8 7 6 5 4 3 2 1 and the sign 0. “With these nine figures…any number may be written.” He gave numerous examples to demonstrate its application, with a variety of rhetorical algebra problems, “explaining in words the desired solution, rather than solving explicit equations as we would do today.” Fibonacci gave several versions of problems along with a choice of several methods of solution.
At the beginning of the book, he added the following apology:
“If by chance I have omitted anything more or less proper or necessary, I beg forgiveness, since there is no one who is without fault or circumspect in all matters.”
Here is an example of one of the problems that appear in Liber abaci (as translated in the book Leonardo of Pisa and the New Mathematics of the Middle Ages by Joseph and Frances Gies.
A man whose end was approaching summoned his sons and said:
“Divide my money as I shall prescribe.” To his eldest son, he said, “You are to have 1 bezant (a gold coin first struck at Byzantium) and a seventh of what is left." To his second son he said, “Take 2 bezants and a seventh of what remains.” To the third son, “You are to take 3 bezants and a seventh of what is left.” Thus, he gave each son 1 bezant more than the previous son and a seventh of what remained, and to the last son all that was left. After following their father’s instructions with care, the sons found that they had shared the inheritance equally. How large was the estate?”
The algebraic (modern) solution and Fibonacci’s rhetorical solution to this problem is as follows:

The Fibonacci Sequence
Many students of mathematics, the sciences, and the arts may recognize the next problem and its association to the famous mathematician, Fibonacci. It is listed in Chapter XII in Liber abaci.
A certain man put a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be provided from that pair in a year if it is supposed that every month each pair begets a new pair which from the second month on becomes productive?
We start with one pair. After the first month, the first pair gives birth to another pair, then, there are two. In Figure 27, a mature pair is represented by a large rabbit symbol and a young pair with a small symbol. After the second month, the mature pair gives birth to another young pair, while the baby pair matures. Now there are three pairs, as depicted in the figure. After the third month, each of the two mature pairs gives birth to another pair, and the baby pair matures, so there are five. After the fourth month, each of the three mature pairs gives birth to a pair, and the two baby pairs mature, giving us a total of eight pairs. After five months, we have a baby pair from each of the five adult pairs, plus three maturing pairs for a total of thirteen. By now, you understand how to proceed to obtain the numbers of mature pairs, of baby pairs, and of pairs in total in successive months.

(Source: Livio, M. The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number. New York: Broadway Books, 2002.)
Therefore, in any given month (starting with the third), the number of adult pairs is simply equal to the sum of the numbers of adult pairs in the two preceding months. The number of adult pairs, therefore, follows the sequence 1,1,2,3,5,8,13,21… Also, from the figure you can see that the numbers of baby pairs follow the exact same sequence, only displaced by one month. Consequently, the numbers of baby pairs are 0,1,1,2,3,5,8…
The sequence 1,1,2,3,5,8,13,21,34,55,89,144,233…, in which each term (starting with the third) is equal to the sum of the two preceding terms, was appropriately called the Fibonacci sequence in the nineteenth century by the French mathematician Edouard Lucas (1842-1891).
How Does the Fibonacci Sequence Relate to the Golden Ratio?
Examine the Fibonacci sequence, 1,2,3,5,8,13,21,34,55,89,144,233,377,610,987…, and look at the ratios of successive numbers (calculated here to the sixth decimal place):
1/1 = 1.000000
2/1 = 2.000000
3/2 = 1.500000
5/3 = 1.666666
8/5 = 1.600000
13/8 = 1.625000
21/13= 1.615385
34/21= 1.919048
55/34= 1.617647
89/55= 1.618182
144/89=1 .617978
233/144=1.618056
377/233= 1.618026
610/377 =1.618037
987/610 = 1.618033.
Do you recognize the last ratio? As we proceed down the Fibonacci sequence, the ratio of the two consecutive numbers goes from greater to smaller and, eventually, comes closer and closer to the Golden Ratio.
If you define a series of numbers by the property that each term (starting with the third) is equal to the sum of the preceding two, then, regardless of the two numbers you started with, as long as you go far enough down the sequence, the ratio of the two successive terms always approaches the Golden Ratio. This explains how the Fibonacci sequence relates to the Golden Ratio.
The following video puts their relationship into perspective.
Fibonacci- World's Most Mysterious Number
Pacioli and the Divine Proportion
The story of phi leads us, next, to an Italian mathematician who published a famous book in Venice in 1509 called The Divine Proportion. The first volume, Compendio de Divina Proportione (Compendium of the Divine Proportion), contains a detailed summary of the properties of the Golden Ratio, or phi.
In the fifth chapter, Pacioli lists five reasons why he believes that the appropriate name for the Golden Ratio should be The Divine Proportion.
Here are two from the list, according to Mario Livio:
-
That it is one only and not more.
-
Pacioli finds a similarity between the fact that the definition of the Golden Ration involves precisely three lengths (AC, CB, and AB in Figure 24) and the existence of a Holy Trinity: Father, Son and Holy Ghost.
Therefore, Pacioli compares the unique value of phi, or the Golden Ratio, to the fact that unity “is the supreme epithet of God himself.” Consequently, not only does phi exemplify a relationship between mathematics and the universe; it also demonstrates a bond between the universe and God.
Since “a picture is worth a thousand words,” and a video many more, let’s take a look at an explanation of phi:
1.618 Phi, The Golden Ration, God Creator of Heaven and Earth
In the second book of Divina Proportione, Pacioli discusses the divine proportion and its association with architecture and the structure of the human body. He references the work of the Roman architect Marcus Vitruvius Pollio (ca. 70-25 B.C.). Vitruvius wrote:
“…In the human body, the central point is naturally the navel. For if a man be placed flat on his back, with his hands and feet extended, and a pair of compasses centered at his navel, the fingers and toes of his two hands and feet will touch the circumference of a circle described therefrom. And just as the human body yields a circular outline, so too a square figure may be found from it. For if we measure the distance from the soles of the feet to the top of the head, and then apply the measure to the outstretched arms, the breadth will be found to be the same as the height, as in the case of the plane surfaces which are perfectly square.”
Renaissance scholars interpreted this passage as demonstrative of the link between “the organic and geometrical basis of beauty.” This led to the concept of the “Vitruvian man,” a diagram which was inimitably drawn by Leonardo da Vinci and currently resides in the Gallerie dell’Academia in Venice, Italy.
The Vitruvian Man
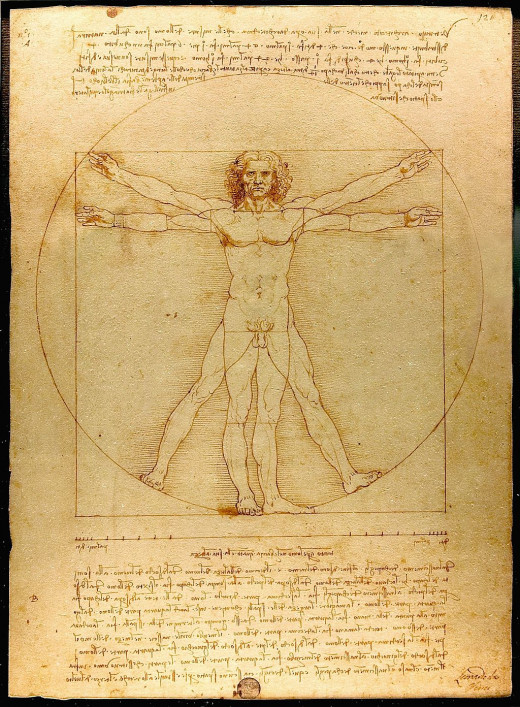
Man’s importance, from his creation by "the most high" in the Garden of Eden and his place at the center of the universe, is depicted in art, from sculpture and painting, to diagrams and books. Most importantly, man is portrayed as an “ideal,” an aesthetic or stylized image of perfect proportion.
The following video demonstrates how the Golden Ratio relates to a mathematical basis for beauty in the human body, as well as the in the universe.
Golden Ratio Human Bodies
The Mystery Surrounding Mathematics
Mario Livio concludes, in The Golden Ratio, that the notion is false that phi provides a universal standard of ideal beauty. He also believes that the use of the Golden Ratio in the construction of the Parthenon and the Pyramids in Giza is unsubstantiated, based on the time period in which these structures were built and an uncertainty that the builders were aware of its existence and had adapted it in their computations.
Was it a deliberate act or a coincidence? One view of the nature of mathematics which, traditionally, is called the Platonic view, is that “mathematics has always existed in some abstract world, for humans to simply discover, just as Michelangelo thought that his sculptures existed inside the marble and he merely uncovered them.”
Mathematicians, such as Kepler, who had religious beliefs that colored their opinions, believed that the universe “is written in the language of mathematics, and its characters are triangles, circles, and other geometrical figures.” Without an understanding of this universal language of numbers and symbols, it is humanly impossible to comprehend it and man is left to wonder in a web of darkness. Did man create mathematics in order to uncover the language of our universe or were the mathematical principles already in place and he was simply enlightened at the appropriate time to discover them?
This begs the question, then, is God a mathematician and does the universe or nature have mathematics at its core? The answers to these types of questions, as well as all the possible correlations between the Golden Ratio and the arts, architecture, music, and so on, are beyond the scope of this article.
What can be stated, in conclusion, is that the ubiquity of phi in nature, the astonishing mathematical properties associated with it, and the incredible manner in which it has inspired, and continues to inspire, thinkers of untold disciplines, attest to its continued relevance, in a universe whose mysterious language continues to unfold.
Thank you for reading this hub. Enjoyed the article? Have any questions or concerns? Leave a comment below or contact me anytime. I look forward to hearing from you.
References
Books
Gies, J., and Gies, F. Leonard of Pisa and the New Mathematics of the Middle Ages. New York: Thomas Y. Crowell Company, 1969.
Livio, M. The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number. New York: Broadway Books, 2002.
Pacioli, L. Divine Proportion. Paris: Librairie du Compagnonnege, 1988.
Internet
http://en.wikipedia.org/wiki/Golden_ratio. Accessed January 10, 2015.
http://en.wikipedia.org/wiki/Mark_Barr. Accessed January 10, 2015.
http://en.wikipedia.org/wiki/Euclid. Accessed January 10, 2015.
www.history.mcs.st-andrews.ac.uk/history/Mathematicians/Pacioli.html. Accessed January 10, 2015
http://en.wikipedia.org/wiki/Liber_Abaci. Accessed February 17, 2015.
http://books.google.com/books/about/Fibonacci_s_Liber_Abaci.html?id=PilhoGJeKBUC. Accessed February 17, 2015.
http://en.wikipedia.org/wiki/Vitruvian_Man. Accessed February 17, 15