Philosophy Simplified: Pre-Socratic Philosophers
Introduction
Philosophy, as any other art of intellectualism, thrives when there's prosperity and enough time at one's hand to just sit down and think, and not fear the next raid, famine or plague. Ancient Greece was a more-than-optimal petri dish for the official birth of philosophy. There had been thoughts and questions before, but the history of real philosophy in Europe starts with an individual called Thales, and with the era of Pre-Socratism (before Socrates).
The rest of my philosophical articles
- Philosophy Simplified: Introduction and Table of Contents
A beginner's guide to philosophy, from Thales to Wittgenstein, from ancient Greece to modern Britain. Each article describes an important topic in philosophy, aimed to teach and entertain.
Thales

Thales lived in Miletos (today Turkey), from 624BC to 546BC, in the middle of Karl Jaspers' axial age. According to an anecdote (either attributed to Diogenes Laërtius or Aristotle), he lived as a politician and a businessman, often called a 'wise' as mockery from the other citizens.
The people of Miletos questioned his 'wisdom': why was he living a modest life, when he knew everything? Definitely mocked, Thales claimed that he enjoyed his life. When asked to show what "his wisdom was good for", he predicted a good harvest of olive by astrology and early meteorology and rented all the oil presses in the Polis.
He was right, but according to Aristotle (or Diogenes, whichever source you prefer), he refused to get rich and declared that he did it solely to prove the usefulness of philosophy.
Another interesting fact is that he took part in the ancient Olympics, and allegedly died from heat stroke during the games (although some sources cite him only watching the games).
Thales' Philosophy
Thales was the first Greek to look for an explanation of the Cosmos (the opposite of chaos, essentially meaning the order of life, reality) outside the mythology. He was looking for the first principle, the arché from which the world originated.
Basically, he tried to define what everything was made of, much like modern nuclear physics, but his answer could be strange to the scientific ear: water. "Nourishment of all things is moist and that even the hot is created from the wet and lives by it." "Water constituted (ὑπεστήσατο, "stood under") the principle of all things." - Thales quoted through Diogenes Laërtius
Other than philosophy, those immersed in mathematics may have nodded at the sight of his name, he has laid down some geometric principles too, like the Thales theorem and the theories of Similiar triangles and Right triangles.
Anaximander
Another philosopher from Miletos (610BC to ??), student of Thales himself. He considered apeiron to be the arché, the former meaning infinite, infinity; he also thought the four elements to be making up the known world.
His cosmology was geocentric, placing the known world in the middle of the universe "just like the demos (citizens) gathers in the agora (market square in the middle of the Polis)". He is considered to be one of the first multi-world thinkers, claiming that "worlds appeared and disappeared for a while, and that some were born when others perished".
There is a legendary speech attributed to him, which includes seemingly random theories about the known world, resembling a madman's prophecies in the middle of Time square. This speech/poem, On nature has been lost over time, traces can be found in other Greek philosophers' works.
Anaximander's On Nature
This work references a "landmass floating on the ocean of world", "thunder resulting from the shock of clouds hitting each other", "rain being humidity pumped up by Sun from Earth", "cosmic wind causing the rotation of celestial bodies", "earthquakes resulting from heavy air descending".
Amongst these is the famous line often referred to by evolutionists, in which Anaximander talks about "Animals first born in warm humidity, then from each other". Sounds great?
"From warmed up water and earth emerged either fish or entirely fishlike animals. Inside these animals, men took form and embryos were held prisoners until puberty; only then, after these animals burst open, could men and women come out, now able to feed themselves."
Now that's more eccentric and Anaximander-like.
Anaximenes

Anaximenes lived from 585BC to 528BC in Miletos, his master being Anaximander himself.
He claimed that the arché was Air, meaning that everything tangible is air. Water is moderately compressed air, while earth is heavily compressed. Rarified air is fire. He defined the celestial bodies as rarified air-exhalations of Earth, patches of fire in space. Not much else is known about him.
Pythagoras

He lived in Croton (Today Italy) through most of his life (570BC to 495BC), Pythagoras considered mathematics and numbers to be the tool to understand our world.
He claimed that the closest thing to the human soul was music, and since music could be defined with mathematical equations (which is would of course be quite hard to swallow for musicians nowadays), the human soul could be interpreted with numbers too.
His followers were the pythagoreans, considered to be the first occult sect, since they met in secrecy and protected the master's teachings from outsiders.
He claimed that celestial bodies were moving according to mathematical equations (which is actually true, with modern science) and believed in mathematically definable reincarnation. According to Diogenes, "Pythagoras heard the cry of his dead friend in the bark of a dog", a mockery of his reincarnation theory.
Along with Thales, Pythagoras is still famous today for his theorem legacy, although some agree that it should be attributed to his sect of mathematicians, not only himself.
Heraclitus
Heraclutus in Ephesus (Today Turkey, 535BC to 475BC), and he is often called the "weeping philosopher" because of his seemingly paradoxical thinking.
"Sen panta rhei - No man ever steps in the same river twice" His philosophy involves the concept of an ever-changing universe, and a reality made up of opposites. He deposited his works into the temple of Artemis, which was later burned down by Herostratos. Therefore only fragments remain from him, sentences quoted by other Greek authors.
Parmenides
He lived Elea (today Italy, 515BC to 460BC) and opposed Heraclitus's idea of an ever-changing, ever-moving universe. He considered sensory perception to be deceiving, an illusion. His only surviving work is a poem, and even this remains in fragments. He claimed that "Existence was necessarily eternal".
Zeno of Elea
Most of Parmenides' ideas were left unanswered, un-debated until his student took matters into his own hands. Zeno, who too lived in Elea (490BC to 430BC), left no works to us intact, his paradoxes are quoted by different authors from ancient Greece.
No traces of his own thoughts remain, yet his paradoxes provide a strange look on physics and Parmenides' ideas. "Motion is nothing but an illusion", this is what he tried to prove with rational arguments, namely his paradoxes, often called the first reductio ad absurdum arguments.
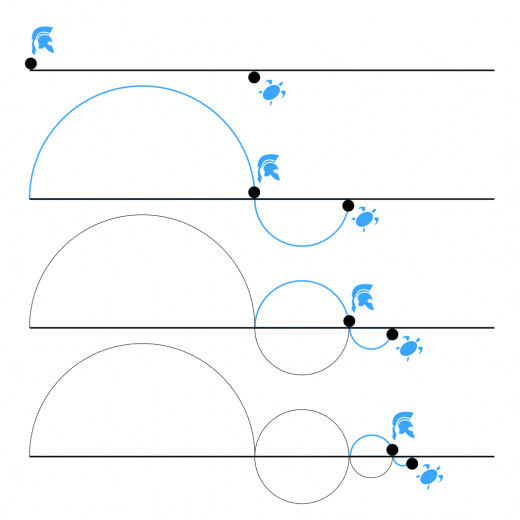
Achilles and the Tortoise
In a race, Achilles is trying to beat a tortoise.
The absurd comes from the fact that "in order to get ahead of the turtle, Achilles has to reach it first. But the moment he reaches it, the turtle has already moved forwards".
No matter how fast Achilles is, the tortoise will always be a step ahead of him. Of course, one could easily claim that Achilles could simply overtake the turtle, but in the original paradox, Achilles' speed is defines as "so fast, that he can jump to wherever the turtle is".
The Arrow Paradox
"If everything when it occupies an equal space is at rest, and if that which is in locomotion is always occupying such a space at any moment, the flying arrow is therefore motionless." - Zeno quoted by Aristotle.
At any time if you pause time while an arrow is flying mid-air, the arrow will stand still. Therefore the arrow's flight is merely made up of moment when the arrow stands still, and therefore motion and movement are merely illusions.
The Dichotomy Paradox
"That which is in locomotion must arrive at the half-way stage before it arrives at the goal." - Zeno quoted by Aristotle.
It takes a finite amount of time to arrive half-way, and then another finite amount of time to arrive half-way from your previous stop to your goal. Eventually, this leads to an infinite amount of finite times required to travel the distance, which Zeno deemed to be infinite.
However, if the paradox is inspected as a numeral series, the answer is clear. The summary of all the finite time-pieces will keep getting closer to the amount of time one required to travel to the goal, rendering the paradox solved.
© 2015 Medvekoma








