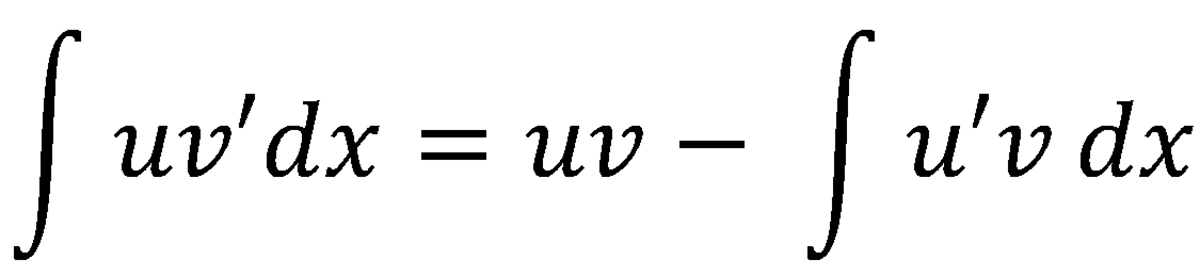Proof of the integral of lnx and other examples involving the integration of natural logs.

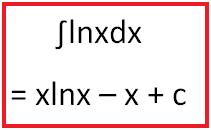
In this hub I will show how to integrate lnx and other functions involving lnx. The best way to integrate lnx is to use integration by parts.

That is the ∫uv’ dx= uv - ∫u’vdx

If you haven’t used integration parts before then you will need to practice this before you attempt the integral of lnx.

Example 1

Work out ∫lnxdx

First rewrite this as ∫lnx.1dx

So u = lnx and v’ = 1. The reason you make u = lnx instead of u = 1 is that you should know the differential of lnx is 1/x. Therefore u’ = 1/x. Also if you integrate 1 you get x so v = x.

Next substitute u = lnx, u’ = 1/x, v = x and v’ = 1 into the above formula for integration by parts:

∫uv’ dx= uv - ∫u’vdx

∫lnx.1dx = lnx.x - ∫(1/x).xdx

Next tidy this up and (1/x) × x will cancel to give 1:

=xlnx - ∫1.dx

Finally, work out the integral of 1.dx

= xlnx – x + c

Example 2

Work out the integral of 2xln5x.

Like example 1 make u = ln5x and v’ = 2x. Always make u equal to the function with natural log.

Now differentiate u to get u’ = 1/x and integrate v’ to get v = x²

Next substitute these values into the formula for integration by parts.

∫uv’ dx= uv - ∫u’vdx

∫2x.ln5xdx = ln5x.x² - ∫(1/x).x²dx

Tidy this up and (1/x) × x² will simplify to x:

=x²ln5x - ∫x.dx

= xlnx – 0.5x² + c

Let’s look at one last example that involves the integration of natural log x.

Example 3

Work out the integral of x³ln8x,

Like example 1 and 2 use the formula for integration by parts:

Just like examples 1 and 2, make u = ln8x and v’ = x³

Now differentiate u to give u’ = 1/x and integrate v’ to give v = ¼x⁴

Next substitute these values into the formula for integration by parts.

∫uv’ dx= uv - ∫u’vdx

∫x³. ln8xdx = ln8x. ¼x⁴ - ∫(1/x).0.25x⁴dx

Tidy this up and (1/x).0.25x⁴ will simplify to get ¼x³

= ln8x. ¼x⁴ - ∫¼x³dx

= ¼x⁴ln8x – (1/16)x⁴ + c

So that is all you need to know about integration involving natural logs.