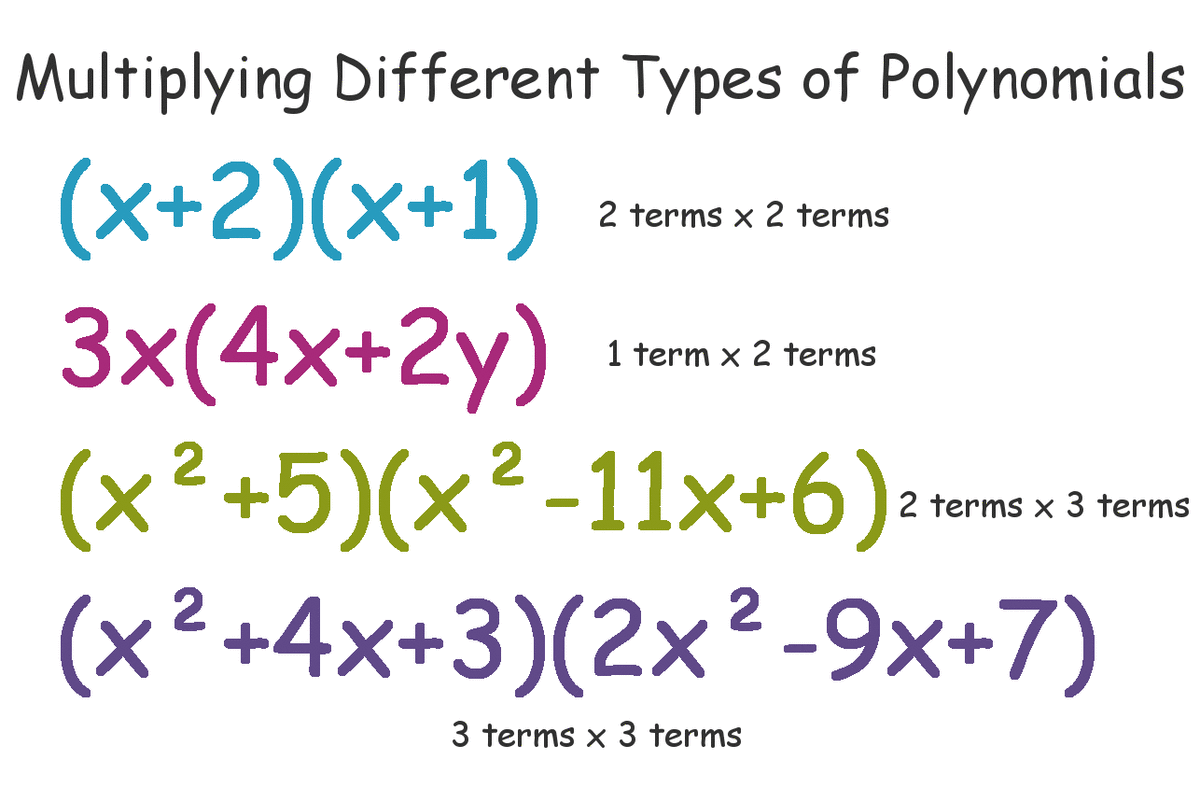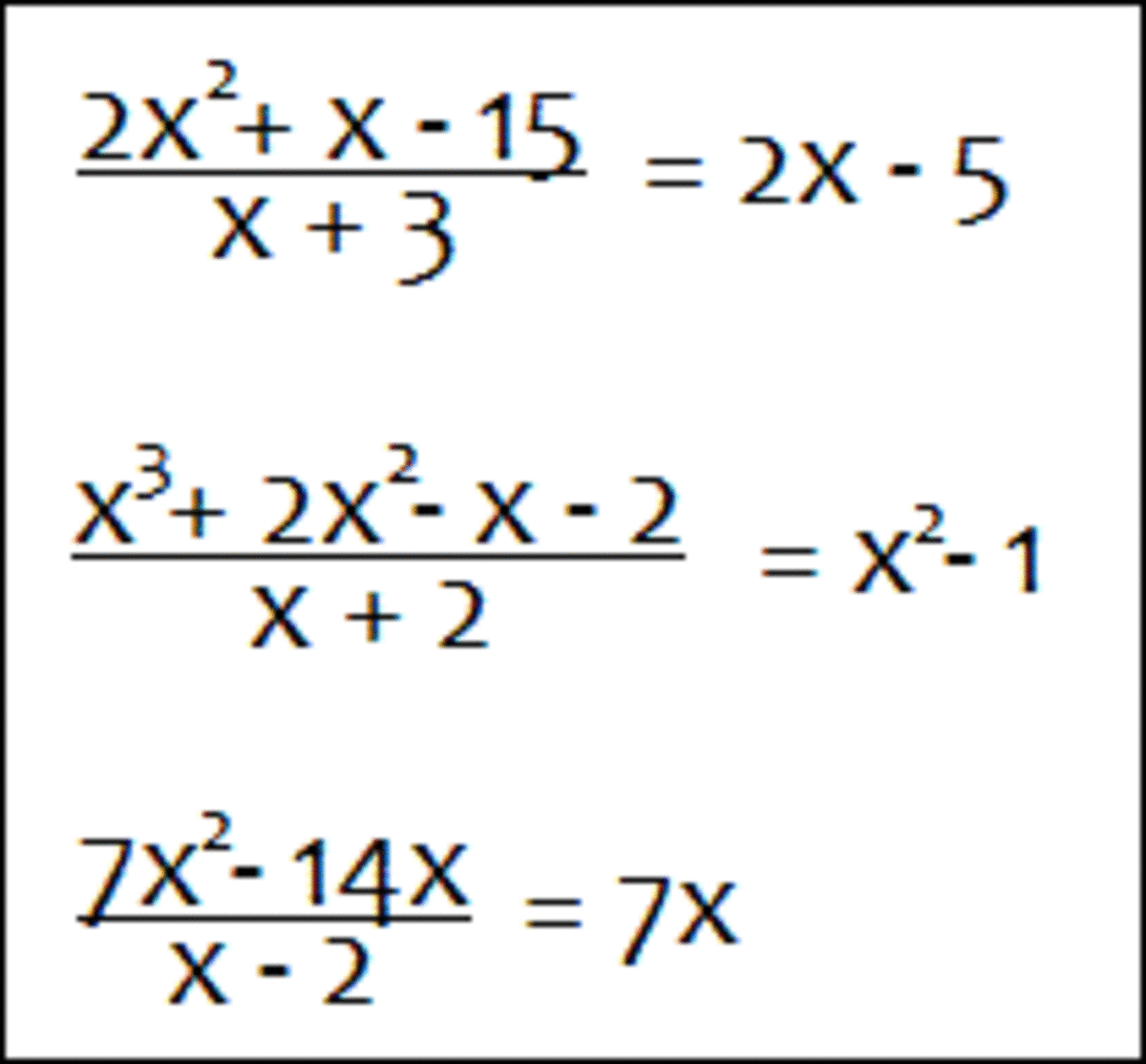College Algebra, Math 163, Notes

Hi everyone,

I am publishing this hub to help anyone who is or will take College Algebra. Information in this hub is strictly from the notes I took from lectures and personal studying. This hub is not intended to teach someone College Algebra, but to aid people who need to refer to information covered in College Algebra. I want everyone reading this hub to know that this hub doesn't completely cover every material in the textbook I used or in every College Algebra class. Also, there may be errors in this hub, so if you find any, please leave me a comment to fix them so this hub won't misguide anyone studying the subject.

Following is some information about the College Algebra class I took.

• Class: College Algebra (Math 163)
• Professor: Randall J. Schmalz
• Semester: Spring 2009
• School: CCBC Essex
• Textbook used: Algebra and Trigonometry Enhanced with Graphing Utilities Edition 5 Sullivan Pearson/Prentice Hall
• Grade I got from the class: A

According to the CCBC (Community College of Baltimore County) mathematics course description, College Algebra explores the nature and scope of college mathematics through the study of functions. Topics include the study of polynomial, rational, radical, piece-wise defined, and absolute value functions and their graphs and applications as well as modeling with these functions. Additional topics include complex numbers, the binomial theorem, inverse functions, operations with functions, and exponential and logarithmic functions and their graphs and applications.

NOTE: 3 credits awarded for MATH 163 (College Algebra) for a CLEP (College Level Examination Program) Precalculus Exam score of 50 or higher.

Prerequisites (One of the following):

• ENGL 052 (Basic Writing II) or ESOL 052 (Academic ESOL)
• RDNG 052 (College Reading)
• Algebra I and II in high school and a satisfactory score on the placement exam
• MATH 083 (Intermediate Algebra)

1. Given y = f(x) and k that is a positive real number, then the graph y = f(x) + k shifts the graph vertically up and the y = f(x) - k shifts the graph vertically down.
2. Given y = f(x) and h > 0, then the graph of y = f(x + h) shifts the graph horizontally left.
3. If y = f(x) is multiplied by a positive real number, then the graph of y = f(x) is:
   vertically compressed (horizontally stretched) if 0 < a < 1
   vertically stretched (horizontally compressed) if a > 0
4. Multiplying f(x) by -1 in y = f(x) gives y = -f(x) which is a reflection about the x-axis
5. When y = f(x) is known, then the graph of y = f(-x) is the reflection about the y-axis.

Review:
Polynomial: any multi-termed expression.

Polynomial function: f(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₁x¹ + a₀ where a_n, a_n-1, ... , a₁, a₀are real numbers and n is a non-negative integer. A polynomial function is smooth and continuous (no sharp corners or cusps, and no breaks).

Degree: the largest exponent of the function.
(example) f(x) = 0 has no degree
(example) f(x) = 2 has degree of 0

Power function of degree n is a monomial f(x) = axⁿ, where a is a real number, a ≠ 0, n > 0, and is an integer.

Properties of f(x) = xⁿ, where n is an even number:
(1) Symmetric about y-axis, even functions.
(2) Intercepts: (0, 0), (1, 1), (-1, 1)
(3) As n increases, the graph becomes more vertical (horizontally compressed) when x < -1 or x > 1.
(4) Domain: all real numbers, Range: { y | y ≥ 0}
(5) Graph is smooth and continuous.

Properties of f(x) = axⁿ, where n is an odd number:
(1) Symmetric about the origin, therefore ƒ(x) is odd.
(2) Intercepts: (0,0), (1, 1), (-1, -1)
(3) Domain: all real numbers, Range: all real numbers
(4) Graph is smooth and continuous.
(5) As n increases, the function becomes more vertical when x < -1 or x > 1 and flattens out between -1 and 1.

1. Factor the numerator and denominator. Find the domain.
2. Rewrite the function in the lowest terms.
3. Locate x and y intercepts.
4. Test for symmetry to the x-axis, the y-axis, and the origin.
5. Find Vertical asymptote(s).
6. Find horizontal or oblique asymptote.
7. Graph with a graphing calculator.
8. Graph by hand.

Logarithm function with base a, a>0, and a≠1, is given by y=log_ax if and only if x=a^y when x > 0

Note:
Domain of log functions = Range of exponential functions (0, ∞)
Range of log functions = Domain of exponential functions (all real numbers)

Properties of Log Functions

1. Domain: {x | x > 0}, Range: all real numbers
2. Graph is smooth and continuous.
3. One-to-one function.
4. Graph is not symmetrial.
5. Increases for a > 1
   Decreases for 0 < a < 1
6. Vertical asymptote at x = 0
7. X intercept at (1, 0)
   No y intercept
8. Graph contains points: (a, 1), (1/a, -1), (1, 0)