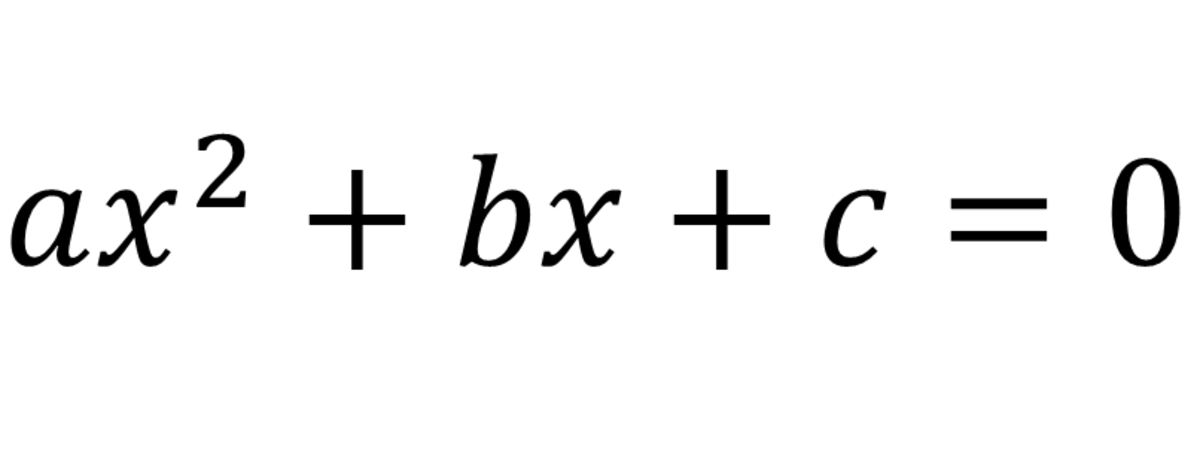Quadratic Equations Rule!!

A Quadratic Equation is a second degree polynomial equation. The word "Quadratic" comes from a Latin word "quadratus", which means "square" and the word "equation" means the process of being equated. The general equation of a quadratic equation is-

ax² + bx + c = 0

here a, b and c are the constants, 'a' is the quadratic coefficient, 'b' is the linear coefficient and 'c' is the constant term. Together they form a quadratic equation. We get two results after solving this equation and they are known as the "roots".

The quadratic equations were first used in Circa in the 8th Century BC in the Sulba Sutras. In 400 BC Babylonian mathematicians and in 200 BC Chinese mathematicians in circa used various methods to solve quadratic equations but the problem they had to face was that they did not have a general formula. In 628 AD, an Indian mathematician named Brahmagupta gave the solution of the quadratic equation but it was not a perfectly general solution. In the year 1896 the general solution was seen for the very first time in the modern mathematical literature in a paper by Henry Heaton.

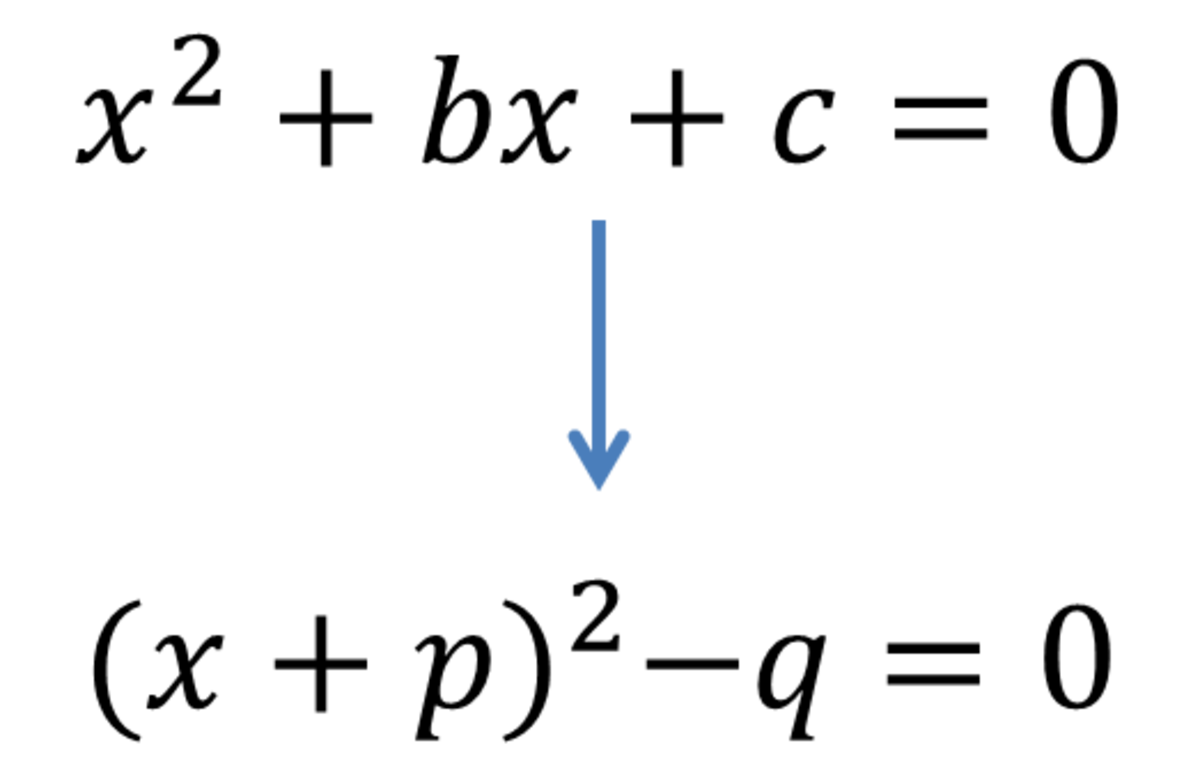
A quadratic equation has two roots as a solution. The two roots can or cannot be distinct and real. The quadratic formula is used to get the roots and it has been derived from the general quadratic equation by the process of completing the square. The formula is stated as:-

x = [ -b ± sqrt(b² - 4ac) ] /2a

here a, b and c have the same meaning. Here the signs ± show that there are two formulas and for each formula exist a root, one is positive and the other is negative.

A quadratic function is a polynomial function. The general form of a quadratic function is as follows-

f(x) = ax² + bx + c

Vertex form and factored form are the two other forms of a quadratic function. All these forms are inter convertable. The solution of both the quadratic equation and the quadratic function are the same roots. If there is a positive discriminant then the graph has two contact points on x-axis, if it is zero then it has only one contact point and if negative then it does not touch the x-axis. The roots of the function f obtained after solving the equation are the x-coordinates of the point of contact of the graph and the x-axis.

To solve a quadratic equation there are many ways but factorisation is the best and the easiest way to solve it. To factorise a quadratic expression means to express it as the product of two factors.

1) a² = a x a

2) ma² + ba = a(m + b)

In the above examples we are factorising the quadratic expressions and converting them into simpler form. If r is the root of the equation ax² + bx + c then the factor of this polynomial would be (x - r). Other ways of solving a quadratic equation are completing the square, by formulae and by graphs. The solutions are of three types-

1) two real solutions :- b² - 4ac > 0

2) one solution :- b² - 4ac = 0

3) complex solution :- b² - 4ac < 0

The complex roots are written in terms of 'i' which is the abbreviation for 'iota' and its value is sqrt(-1).

Often we see higher degree polynomial equations and consider them as being tough but they can be solved by converting them to quadratic form and then solving them. Quadratic equations are very useful as they were used in almost all the major discoveries that have been made till date. They are also used in calculating trajectories in projectile motion. A parabolic antenna also uses quadratic form. Quadratic equation is the fundamental basic of Mathematics as well as Physics. They help in solving a variety of applied and logical problems.