Radian measure - and just what are radians anyway?

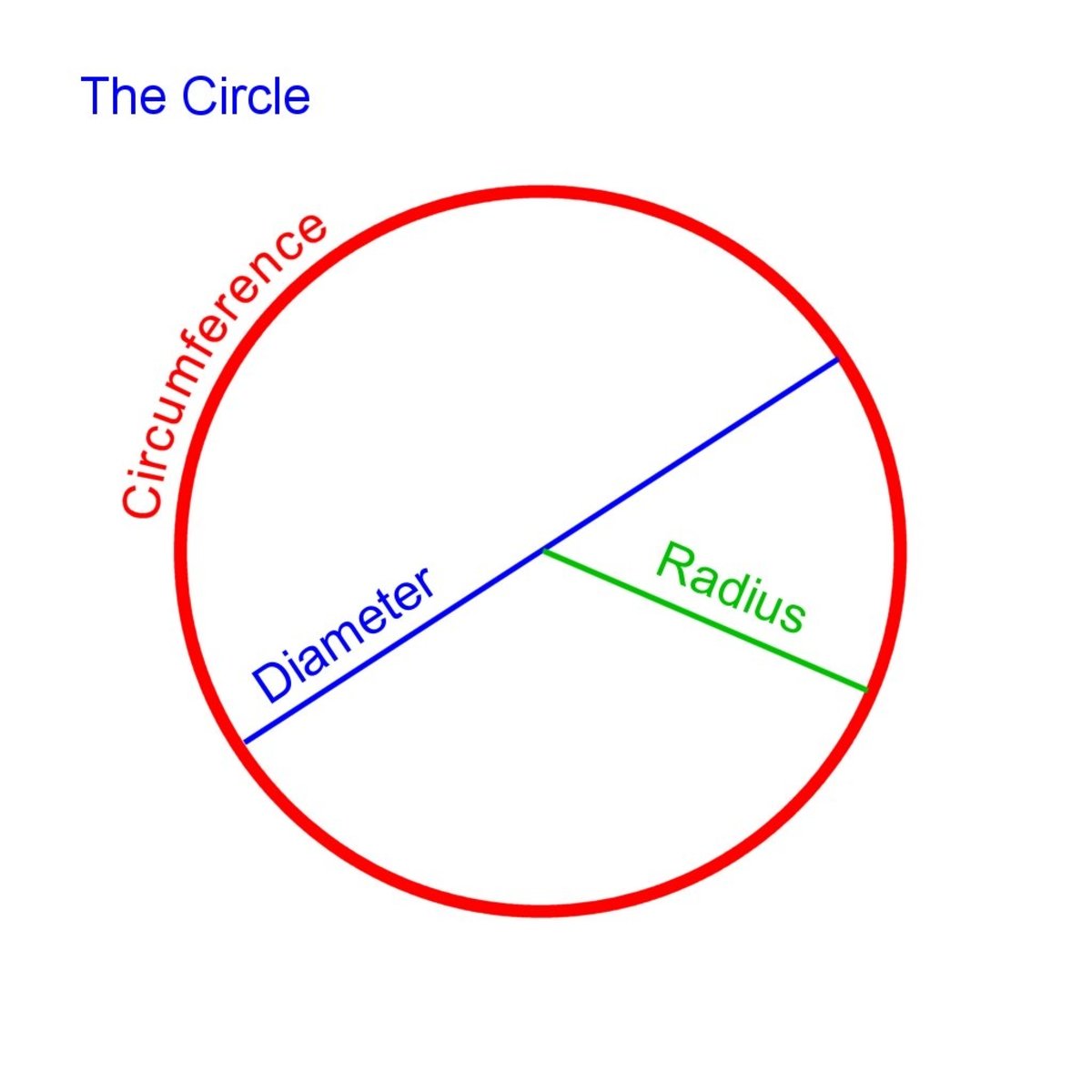
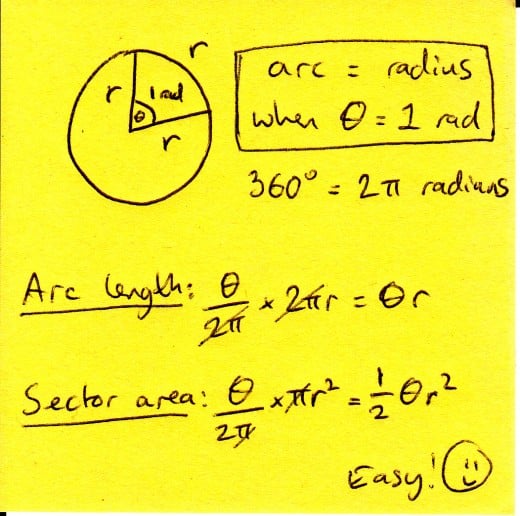
One radian is the angle needed at the centre of a circle to make the arc the same length as the radius of the circle.  A sector taken from a circle where all the sides are the same length (i.e. the perimeter = 3 x the radius) will have an angle of one radian.  Once you get your head round it, radians aren't that bad.

Because the radius goes into the whole circumference 2pi times, there are 2pi radians in a circle.  In other words: 2pi radians = 360 degrees, pi radians = 180 degrees, and so on...

It might seem odd at first, but really it makes more sense than using degrees - which are actually pretty arbitrary measurements when you think about it!

So, how do we find the length of an arc, given an angle in radians?

You should have looked at arc lengths before - if not, they're still pretty simple to work out.  As the sector is a fraction of the circle, the arc will be a fraction of the circumference.  What fraction it is depends on the angle - but it will always be out of 360 degrees, or in this case 2pi radians.

Because the formula for the circumference is 2 pi r, everything cancels down when the fraction's written over 2pi, leaving the length of the arc simply being the product of the angle at the centre and the radius of the circle.  Easy.

Similarly, the area of a sector is found by taking the fraction of the circle we're interested in, and multiplying by the area of the whole circle.

You can see that, again, a lot simplifies down when using radians - leaving us with the area being half the product of the angle and the radius squared.

This can be used to find areas of segments too, if you think of the sector being made of a triangle and a segment together - like a well-licked ice-cream cornet, where the the wafer cone is the triangle and the ice-cream is the segment?

Anyway, we can find the are of the segment by simply subtracting the area of the triangle (half a b sin c) away from the sector.