Rectangles, Properties and mathematical facts of a rectangle (oblong)
A rectangle is probably one of the first shapes you recognise, but knowing all of the mathematical of a rectangle is a little trickier. Here are the main mathematical properties of a rectangle, many obvious but others less so.
A rectangle is a quadrilateral as it is a shape with 4 edges.
The opposite sides of a rectangle are equal in length.
A rectangle contains 4 right angles.
A rectangle also has 2 lines of reflectional symmetry (vertical and horizontal through the centre)
The order of rotational symmetry of rectangle is of order 2 – so a rectangle has rotational symmetry.
You can draw 2 diagonals inside a rectangle. The angles made in the centre of the shape by the diagonals are not right angles (unless the rectangle is a square). The length of the diagonal of a rectangle can be found by using Pythagoras theorem.
Example
Work out the length of the diagonal of a rectangle that is 4cm long by 3cm wide.
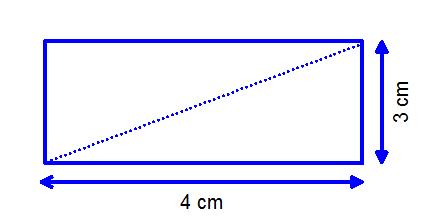
4² = 16
3² = 9
16 + 9 = 25
√25 = 5cm
So the length of the diagonal of the rectangle is 5cm.
The area of a rectangle can be worked out by multiplying the length and width of the rectangle together. So for example, if you have a rectangle that is 9cm by 6cm then the area will be 9 × 6 = 54 cm².
The perimeter of a rectangle can be found by adding the length and width of the rectangle together and doubling this answer.
Example
Work out the perimeter of a rectangle that is 13cm long and 8 cm wide.
First add up the length and width 13 + 8 = 21.
Now double this answer 21 × 2 = 42 cm
So the perimeter of a 13 by 8 centimetre rectangle is 42cm.
Also, a rectangle is one of the easiest shapes that you can tessellate. You will find this pattern on many floors and garden areas around the world.