Simple Harmonic Motion (SHM) A-level Physics Revision

Simple Harmonic Motion is something that we see around us every day however don't really notice. If you see a tree swinging in the wind then that in its most basic form is SHM. Any pendulum that swings follows SHM.
Definition
The term Simple Harmonic motion sounds very complex however in reality it isn't, the defnition of SHM is; When the the acceleration of an oscillating body is directly proportional to minus of it's displacement from the equilibrium, Or in other words if the pendulum is at the centre its acceleration is zero because the displacement is zero, when the pendulum is at its furthest point either way then it's aceleration is at its biggest (Or smallest if you count direction), and when the displacement is halfway then the acceleration is half way also. The diagram I have drawn bellow shows show each parameter varies at each point on a oscillation

Equations
Simple harmonic motion is quite a maths dependant topic, so there are a few equations you need to be able to use. They should give you these in the exam formula sheet however you should know about them before that.
Acceleration = ((Angular Speed)^2) x Displacement
Displacement = Amplitude x Sin(2pi x Frequency x Time)
Velocity = (+-)Angular Speed x ((Amplitude^2 - Displacement^2)^1/2)
Time Period = 2pi((Length of Pendulum/Gravitational Constant)^-1/2) Or if for a spring then its Mass/Spring constant.
NOTE
These equations assume that the oscillation is a "free oscillation" where there is no friction. In practice you will have friction however this should be kept to a minimum where ever possible.
As the diagram shows, the acceleration is the opposite of displacement (Antiphase) which corresponds to the definition of SHM. It also shows that the force on the pendulum at is directly proportional to the acceleration, this is due to the equation Force = Mass x Acceleration (F=MA).
What effects an oscillation?
If you look at the equation on the left for time period of a pendulum then you will realize that they don't include the Mass or the Angle. The reason for this is because Mass and Angle swung don't effect the time period of the oscillation.
- If you swing a larger angle it will still take the same time to return, it will just be moving faster as it crosses the equilibrium.
- If you add a larger weight to the end of the pendulum then it will still take the same time to return, the added mass just means that there is more mass to slow down and speed up each time, however these cancel each other out.
Energy
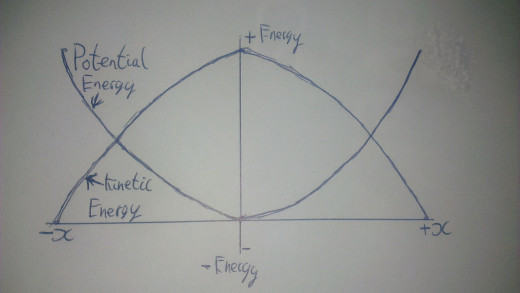
Assuming that the oscillation is a free oscillation and thus no energy is lost then the total energy in the system must remain constant throughout the whole cycle. This energy is split between the Kinetic Energy of the pendulum moving and the Gravitational Potential Energy. When the velocity is zero all of the energy is either in gravitational potential or elastic potential (if a spring is used). As the oscillation passes the equilibrium then all of the potential energy has been transferred into kinetic energy. However at all points the total energy is the same. As shown in this diagram.
Damping
For energy to be lost (in any case where it is not a free oscillation) then there has to be damping. This can be air resistance or anything that causes the oscillations to decrease. A real life example of damping is in a car suspension system where shock absorbers stop the spring from continuing to "bounce" after going over a bump. There are 3 types of damping:
- Critical Damping, This is the optimum situation where the oscillation stops in the quickest possible time.
- Overdamping, This is when the damping is too heavy and causes the osscilation to struggles to return to the equilibrium.
- Light Damping, This is when the damping has little effect and the oscillations continue but with smaller amplitudes each time.
Resonance
Resonance happens when you have one oscillation driving another at exactly the objects natural frequency. For example on a swing, the swing will only start to oscillate a large amount when the driving force from the person on the swing is in phase with the natural frequency of the swing. You can sometimes also observe this with sound where a certain frequency might seem to make a room resonate. This can be linked back to damping above, the heavier damped the system is the less effect resonance has.
Hope you have found this guide to Simple Harmonic Motion useful.