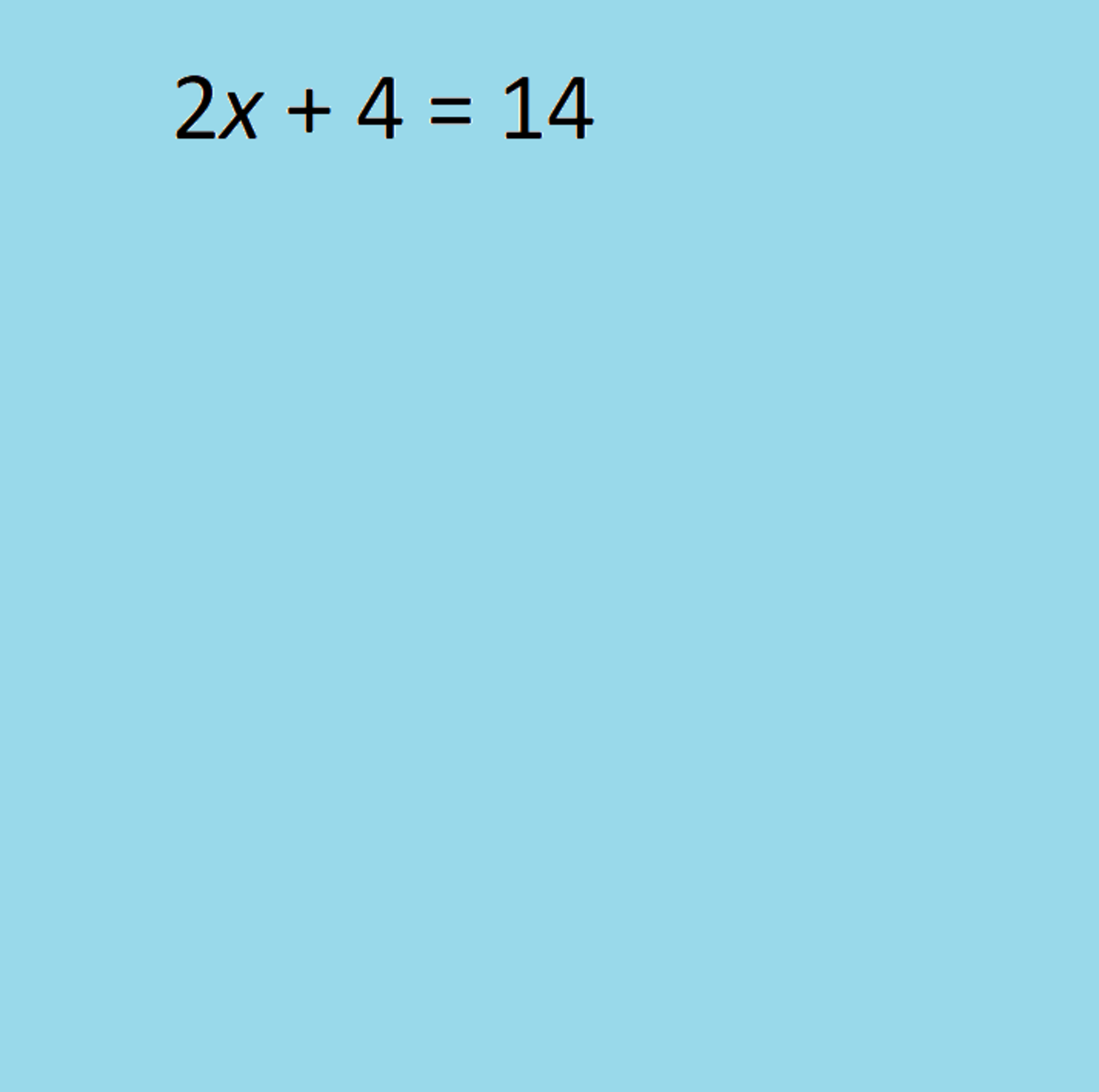Solving Quadratic Equations By Using Quadratic Formula
Solving Quadratic Equations By Using Quadratic Formula
Quadratic equations is one of the most important concept in Algebra. It is of great importance to gain skill in solving quadratic equations. As a general rule, we may solve a quadratic equation most simply and quickly if we first try to factor the equation. If it cannot be readily factored using quadratic formula is the next best way. The formula works not only for integers a, b and c but for any real number. It works even if the coefficients are complex numbers.
The solutions for the quadratic equation aX^2 + bX + c = 0 are :
X = ( -b +- SQRT( b^2 - 4ac) ) /2a
Example One : Solve the equation 30X^2 + 49X + 20 = 0
To solve this equation we first identify a = 30 b = 49 c = 20
Then substitute the corresponding values in the formula :
X = (-49 +- SQRT ( 49^2 - 4 (30) (20) ))/2(30)
X = ( -49 += SQRT ( 2401 -2400) )/60
X 1 = ( -49 + 1)/60 = -48/60 = -4/5
X2 = ( -49 -1)/60 = -50/60 = -5/6
Example Two :
25X ^2 - 30X + 13 = 0
a = 25 b = -30 c = 13
X = ( 30 +- SQRT ( 30^2 - 4 (25) (13) ) )/2(25)
X = (30 +- SQRT(900 – 1300))/50
X = ( 30 += SQRT (-400))/50
X = (30 += 20i)/50
X1 = (30 + 20i)/50 = 10 (3 + 2i )/50 = (3 + 2i )/5
X2 = ( 30 - 20i )/50 = !0 (3 – 2i )/50 = ( 3 – 2i)/5
Example Number Three :
Solve for the equation X^2 + 4iX - 5 = 0
a = 1 b = 4i c = -5
X = ( -4i +- SQRT( (4i)^2 - 4 (1 ) (-5)) )/(2)(1)
X = ( -4i +- SQRT( -16 + 20))/2 since i^2 = -1
X = ( -4i +- 2)/2
X1 = ( -4i + 2)/2 = 2(-2i + 1)/2 = -2i + 1
X2 = (-4i - 2)/2 = 2(-2i – 1 )/2 = -2i - 1
SOURCE: COLLEGE ALGEBRA By :
REES
SPARKS
REES