Solving a Quadratic Equation by Using the Quadratic Formula
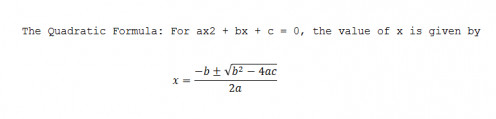
Do you know the Quadratic Formula?
The origins of the Quadratic Formula
Sometime in the annals of history someone realized that they were solving quadratic equations by completing the square – each time the method was identical and thus using algebra they managed to create a formula that could be used instead of the individual steps.
The formula above is the result and it is one of the most used formulas in mathematics. The quadratic formula will always produce an answer (even if there are imaginary numbers involved) and helps solves equations that cannot use other methods such as factorization.
Example of Quadratic Formula being Used
The idea of the quadratic formula is to isolate the unknown variable (in this case X) and perform calculations on the known constants (A, B and C). The process is identical every time and as long as you remember the quadratic formula you will be able to solve any quadratic equation especially when other methods fail. Once used often you'll find the quadratic formula will be the easiest to utilize.
X2 – 10X – 24 = 0
Comparing this to the formula aX2 + bX + C = 0 we get a=1, b=-10 and C=-24.
Inserting these values into the quadratic formular we get:
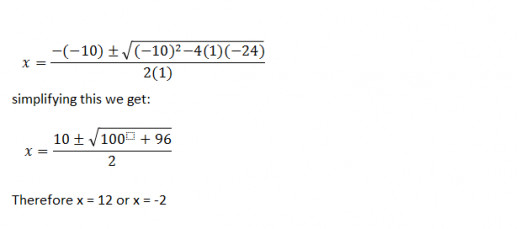
If you insert both values in the original formula you will see that both are valid and solve the equations. While both are valid answers, in this case as we were calculating the dimensions of a lawn then the only valid answer will be x = 12 as a lenth cannot be less than zero.
Potential Problems with the Quadratic Formula.
One of the perceived problems with the quadratic formula is that the equation within the ‘Square Root’ could be negative – in normal mathematics we cannot calculate the square root of a negative number.
However, this is where the concept of i comes in. i is an imaginary number and is defined as the square root of -1. Thus when evaluation the Quadratic Formula you will be able to come up a solution that may sometimes be evaluated as an imaginary number but when this number is inserted into the original equation it produces the desired result.
Tips for using the Quadratic Formula
- Always get the expression in the format aX2 + bX + C = 0; if you don’t make the formula equal zero, the calculation will fail.
- Double check your results by inserting them back into the original quadratic equation.
- Use standard rules to evaluate the quadratic formula. BODMAS or PEMDAS are instructions on the order in which you should evaluate a formula (Brackets, Of, Divide, Multiply, Add, Subtract) or (Parenthesis, Exponents, Multiply, Divide, Add, Subtract).
- Don’t Panic! – probably the most important advice – the quadratic equation may seem complicated but it is very easy to use and will give the correct solution every time.