Solving dimension problems in Physics
When you are solving problems of dimension in Physics you have to be quite thorough with formulae. All the formulae of complex physical quantities should be at your finger tips.
Following are a few problems on dimensional representation of units of physical quantities. For your convenience they are solved. You are advised to solve them with a close watch on the time that you take:

Problem 2.
If work done ‘W’, acceleration ‘A’ and length ‘L’ are chosen as the three basic quantities how will mass be known in terms of basic units?
Solution:
Work done= Force X displacement
=Mass X Acceleration X displacement
Therefore,
Mass may be represented by Mass= (Work done)/ (Acceleration X displacement)
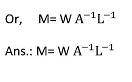



Problem 6.
Express Tesla in basic units.
Solution:
We use Tesla as the unit of magnetic Flux Density. Expressing it in terms of basic units requires use of Lorentz Force Law which states that when a charged particle moves in presence of electric and magnetic fields, the force on it is given as:
F=q(E+v X B) where F=Force, q=Electric Charge, V=Velocity, B=Magnetic Flux Density.
If there is no electric field, the equation reduces to F=q v X B
From this, in terms of basic units,
Tesla=(Newton)/(Coulmb. m/s)
Writing Newton= (kg.m.)/ s2, we get,
Tesla=(kg.m)/s2 / (Coulmb. m/s)
=Kg/ (Coulomb.sec)
=kg/ A.s2 (since Coulmb=A. sec)
Conclusion
One should solve various kinds of problems even on easy looking chapters. Dimension problems are generally easy ones. But having thorough knowledge of dimensions helps. Sometimes formulae can be reproduced with the help of dimensions. Here I did not solve any dimensional problem with electrical quantities. You should practise those too.