Standing Waves in a String


Introduction to the Whole Shebang
Under the Christmas tree, a few years ago, my son opened a package that turned out to be a guitar. When he removed it from the box it was broken and we had to ship it back to the manufacturer for a replacement.
He waited patiently, well as much as a six year old can muster, and was rewarded a few months later with a new guitar in the mail.
At first he didn't really understand how to play the instrument and he would strum the strings in a random fashion and pretend he was a rock star.
I sat down with him and showed him how to strum the strings with a pick and how to pluck the strings individually. I am not a guitar player but I new a few key components that I was able to show him.
We have moved to another home since then and his guitar is packed away for now. But I figured that the ownership of the instrument warranted a look at how waves on strings operate in the physical world.

What are Waves?
In this hub we are primarily looking at waves on a string. Not only waves on a string but waves produced by the pluck of a guitar string.
Let us consider a wave. A wave is simply the motion of a disturbance through space or a guitar string. Each disturbance carries with it energy and momentum that will continue as a wave through whatever medium it is travelling through.
A wave has three characteristics. These three characteristcs are wavelengths, frequencies, and speeds or velocities.
The equation for a wave is the wavelength, Lambda or (w), times the frequency, f, equals the velocity, v.
(w) x f = v
A travelling wave or transverse wave are when the particles of disturbance move perpendicular to the wave velocity. A standing wave on a string would be a travelling or transverse wave.
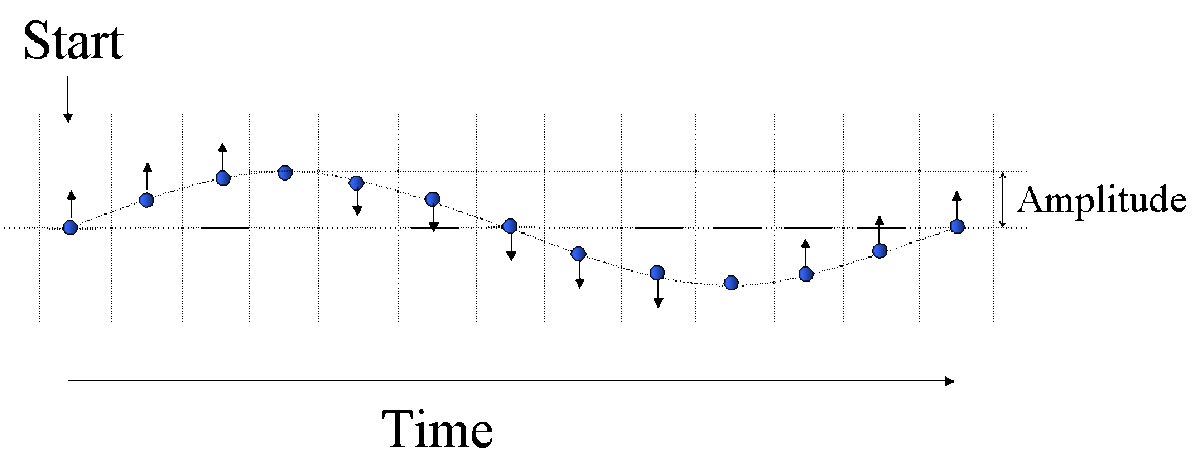
The curved shape of the vibrating string is called the waveform. The high point of the waveform is called the crest and the low point is called the trough.
Each particle of the string oscillates vertically in the y-direction with simple harmonic motion.
The amplitude of the wave would be considered the maximum distance the string is raised above equilibrium if equilibrium is considered a string with no wave. Amplitude is measured by looking at the distance between crest and trough.
The wavelength is the distance from one crest to another. A wave period is how long it takes to get through one oscillation.
When two waves meet they interfere and combine causing a superposition of two interfering waves. Look at the pictures located to the right these would be an example of two interfering waves.
Nodal points or nodes are where interfering waves are stationary. Antinodes are the areas on the wave of maximum displacement.
Only certain frequencies produce standing waves, given the tension, density, and length of the string. The string tension and mass will effect standing wave patterns. The frequencies that produce standing waves are called natural frequencies or normal modes of oscillation.
The lowest natural frequency, f(1), is called the fundamental frequency or the first harmonic. Each frequency above the first harmonic would be the second, third, fourth, etc. (f(2), f(3),f(4)...)
A Conclusion
Each string on the guitar has a different density and tension and as you pluck each string you will get a different frequencies or harmonics.
When these different frequencies or harmonics are used individually as notes or combined into chords music is created.
One day when we are done living out of boxes my son will have his guitar back in his hands and I will explain to him how each string has its own frequency and how each frequency can combine to make music.
He probably will look at me with a blank expression for a few seconds and then he will continue to practice his strum and maybe a note here or there.
A beginner book by Mel Bay probably will help him with his desire to learn to play the guitar more than my physics lesson ever will. That is the way of the world.