Stationary points. How to find a stationary point on a graph (turning points)
A stationary point (or turning point) is the point on the graph where the gradient is 0.
That is a stationary point occurs when f´(x) = 0
So to find a stationary point:
1) Differentiate f(x) to give f´(x)
2) Make f´(x) = 0 and solve this equation.
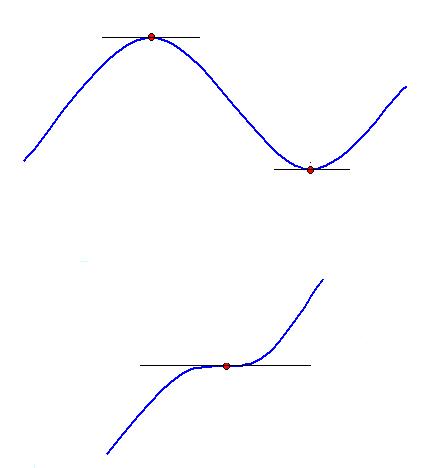
Example 1
Find the x coordinate of the stationary point on the graph f(x) = 7x² - 3x + 5
Let’s follow the 2 steps outlined above:
1) Differentiate f(x) to give f´(x)
f´(x) = 14x -3
2) Make f´(x) = 0 and solve this equation.
14x – 3 = 0
14x = 3
x = 3/14
So the turning point of this graph occurs at x = 3/14
Example 2
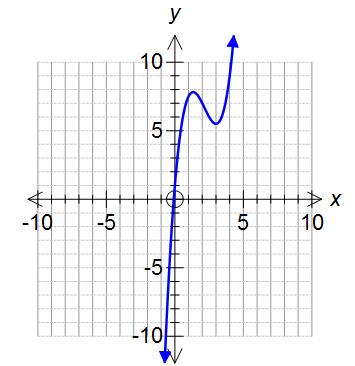
Find the x coordinates of the stationary points on the graph f(x) = x³ - 6.5x² + 12x + 1
Again, to find the stationary points follow the 2 steps above:
1) Differentiate f(x) to give f´(x)
f´(x) = 3x² - 13x + 12
2) Make f´(x) = 0 and solve this equation.
3x² - 13x + 12 = 0
Since you are left with a quadratic it needs to be factorised before it can be solved.
3x² - 13x + 12 = (3x -4)(x-3)
So either 3x-4 = 0 or x -3 = 0
So x = 4/3 or x = 3.
If you draw the graph of f(x) = x³ - 6.5x² + 12x + 1 then you can see that these 2 points are correct.
To verify the nature of a stationary point (either min, max or inflexion) you need to calculate the second derivate. I will write about this in a hub shortly.