Stellar Numbers General Formula (Part 3)

To complete our next task I should use other values of p to check general statements and expressions. For that task I will use 5 as value for p.

p = 5

I have made initial four stages of stars with 5 vertices:

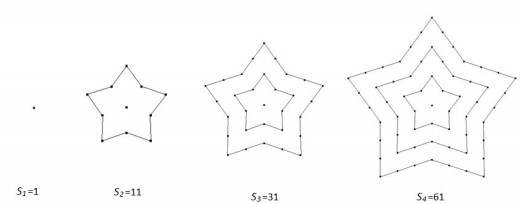
One more time I put data in the table for easier usage of data but this time I realized it is easier to put number of dots in each new ring (U_n)without step by step calculations.

From this table it is easy to see what is the difference in between each ring. By using this formula it is easily calculated too: d=U_n-U_n-1. So, we can calculate that and difference in this case is 20-10=30-20 => 10=10 so this difference is constant in this sequence and it is still arithmetic one. Now when we know what is the difference between each ring we can calculate how many dots is there in next ring and by that calculate how many dots there is in next stage of this diagram. So U₅ = U₄ + d => U₅ = 30 + 10 => U₅ = 40 and simply we add this ring to the others and we get: S₅ = S₄ + U₅ => S₅ = 61 + 40 => S₅ = 101. We can use the same principles for finding S₆ where U₆ = U₅ + d => U₆ = 40 + 10 => U₆ = 50. When we found this number we can find S₆ easily by adding that ring to the previous ones. So, S₆ = U₆ + S₅ => S₆ = 50 + 101 => S₆ = 151.

When we found those numbers we can easily make diagrams for stages S₅ and S_6, those would look like this:

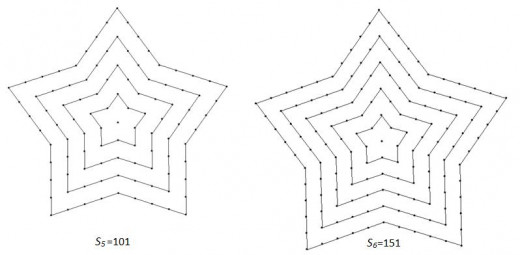
The next thing is to make simple pattern up to stage S₇ and that would look like this:

• S₂ = S₁ + 1 · 10
• S₃ = S₂ + 2 · 10
• S₄ = S₃ + 3 · 10
• S₅ = S₄ + 4 · 10
• S₆ = S₅ + 5 · 10
• S₇ = S₆ + 6 · 10

Since we have formula for S₇ we can calculate it by introducing known variables in it. So, that would look like this: S₇ = 151 + 6 · 10 => S₇ = 151 + 60 => S₇ = 211.

Our next task was to find general statement for 5-stellar number at stage S_n in terms of n. That can be figured out by pattern which we used in previous task and in that pattern we can see that every time there are few common things. That number which multiplies 10 is always lower than n by one. So from that we can get formula which says: S_n = S_n-1 +(n-1) · 10

• n=7; S₇ =211

• 211 = 151 + (7-1) · 10
• 211 = 151 + 6· 10
• 211 = 151 + 60
• 211 = 211

• n=5; S₅ = 101

• 101 = 61 + (5-1)·10
• 101 = 61 + 4 · 10
• 101 = 61 + 40
• 101 = 101

In my opinion the final goal of this portfolio is to make general expression which can be used for any stellar number. In this task I should do that and produce the general statement, in terms of p and n, that generates the sequence of p-stellar numbers for any value of p at stage Sn.

In sequences that I worked with in the previous task I found general expression in terms of n. So that formulas would be:

When it was star with 6 vertices formula was:

S_n = S_n-1 +(n-1) · 12

Then later on there was star with 5 vertices and formula was:

S_n = S_n-1 +(n-1) · 10

While examining the general statements we can see that the form of those statements are mainly same, the only difference is in the last number which changes with the number of vertices. Those numbers are directly connected to the vertices because each vertices has 2 sides and each ring (each new star) gain one more dot on each side and those numbers can be presented:

For 6-stellar number 12 can be presented like 6x2 and that is because there are 6 vertices and each side of vertices gets one dot

For 5-stellar number 10 can be presented like 5x2 and that is also because there are 5 vertices and each side of vertices gets one dot

From these observations we can made one general formula which looks like this:

S_n = S_n-1 +(n-1) · p · 2

The scope or limitations of the general statement:

-the biggest limitation of this general statement is that you need sum of the terms before the term you need and that is the biggest problem of this general statement

- n can't be 0

- n can't be 1

- The statement applies only to stellar where p is in the group of Natural numbers

- The general statement applies only to stellar shapes

- n must be in group of Natural numbers