Synthetic Division: Algebra Division Made Easier
As a mathematics instructor, I enjoy being able to teach a topic that makes the algebra student's life a little easier. But teaching really becomes fun when the topic not only makes life easier, but there are also several useful applications to the topic. Synthetic division is not only a topic like that, but the process is pretty easy. There is, however, a catch. Synthetic division only works with linear divisors of the form x-k, where k is a constant. There cannot be any exponents on the variable except 1 and the coefficient on the variable has to be 1. If either of these is not the case, then long division should be used.
Synthetic Division Steps
The following are the steps to perform synthetic division. If these steps do not make sense at first, look at the example in the next section.
- In a row, write down the coefficients of the polynomial in the numerator. If there are any missing terms, a zero must be put in for the missing term. For example, x3 + 2x - 3 is missing an x2 term. So we need to add that as x3 + 0x2 + 2x - 3. If this is not done, the answer will be completely off after the point of the missing term.
- Off to the left of the line of coefficients, put whatever number k is into a box. Notice the denominator must be of the form x - k. So if the denominator is x - 2, k is 2. If the denominator is x + 3, k is -3 because the denominator is really x - -3.
- Draw a horizontal line below the row of coefficients, leaving enough room between the line and the row of coefficients to write another row of numbers.
- Bring the first coefficient down below the line.
- Multiply the last number brought down below the line with the box number. Write the result in the next column above the line.
- Add the two numbers above the line and write the result below the line.
- Repeat steps 5 and 6 until done.
- Box in the last number brought down in the last column.
- The last line is the answer to the division problem after subtracting one from each of the exponents. The boxed in number is the remainder.
Now for an example.
Synthetic Division Example
Suppose we have the following problem.
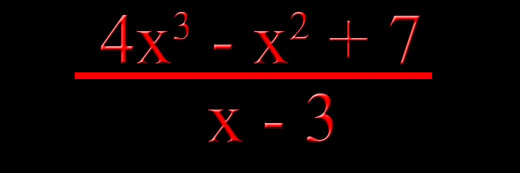
The first thing to note is the x term is missing. So we first put that in with a zero:
4x3 - x2 + 0x + 7.
Step1: Write the coefficients of the numerator in a row without the variables.

Step 2: Put k in a box to the left.
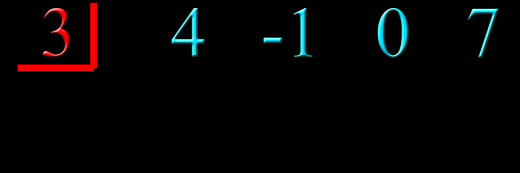
Step 3: Draw a line below the coefficient row, leaving row to write another row of numbers.

Step 4: Bring the first coefficient down below the line.
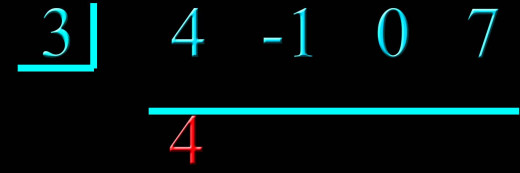
Step 5: Multiply the last number brought down (4) with the box number (3) to get 12. Write this in the next column above the line.

Step 6: Add the two numbers above the line and write the result below the line.
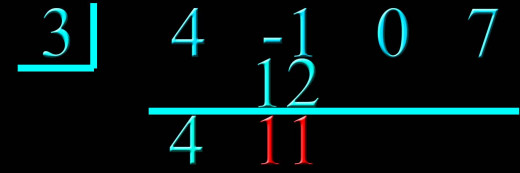
Back to step 5: Multiply the last number brought down with the box number and write the result in the next column above the line.
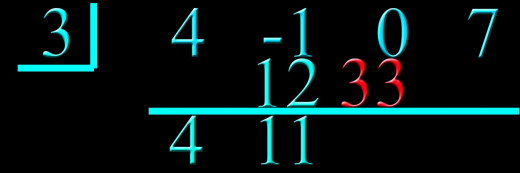
Step 6: Add the two numbers above the line and write the result below the line.
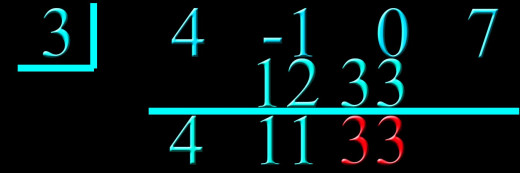
Back to step 5: Multiply the last number brought down with the box number and write the result in the next column above the line.
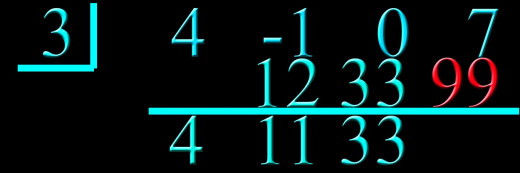
Step 6: Add the two numbers above the line and write the result below the line.
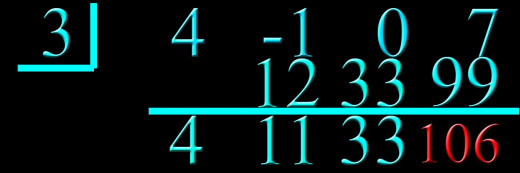
Step 8: Box in the last number brought down in the last column.
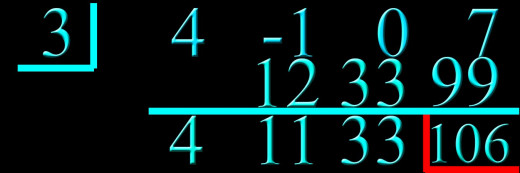
Step 9: The last line is the answer to the division problem after subtracting one from each of the exponents. The boxed in number is the remainder. In this example, the 4 in the top row had an x3 behind it. Since we divided by x - 3, the 4 in the bottom row now has an x2 behind it. The -1 in the top row had an x2 behind it in the original problem. So the 11 in the bottom row now has an x behind it. The zero in the first row originally had an x behind it, so the 44 in the bottom row is now a constant. The number in the box, 139, is the remainder and still has to be divided by the original denominator. So when it is all pieced together, the answer should look like this:
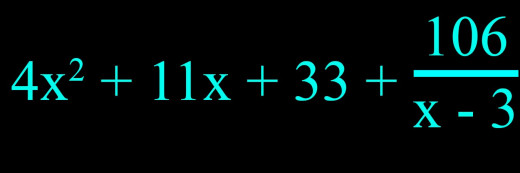
Concluding Remarks
Synthetic division is a very quick and easy way to divide a polynomial by a binomial of the form x - k. This is just one of several uses for synthetic division.